Solving a time-dependent problem#
This notebook will show you how to solve a transient problem using DOLFINx, and highlight differences between legacy DOLFIN and DOLFINx. We start by looking at the structure of DOLFINx:
Relevant DOLFINx modules:
dolfinx.mesh: Classes and functions related to the computational domaindolfinx.fem: Finite element method functionalitydolfinx.io: Input/Output (read/write) functionalitydolfinx.plot: Convenience functions for exporting plotting datadolfinx.la: Functions related to linear algebra structures (matrices/vectors)
Creating a distributed computational domain (mesh)#
To create a simple computational domain in DOLFINx, we use the mesh generation utilities in dolfinx.mesh. In this module, we have the tools to build rectangles of triangular or quadrilateral elements and boxes of tetrahedral or hexahedral elements. We start by creating a rectangle spanning \([0,0]\times[10,3]\), with 100 and 20 elements in each direction respectively.
from mpi4py import MPI
length, height = 10, 3
Nx, Ny = 80, 60
extent = [[0.0, 0.0], [length, height]]
domain = mesh.create_rectangle(MPI.COMM_WORLD, extent, [Nx, Ny], mesh.CellType.quadrilateral)
In constrast to legacy DOLFIN, we work on simple Python structures (nested listes, numpy arrays, etc).
We also note that we have to send in an MPI communicator. This is because we want the user to be aware of how the mesh is distributed when running in parallel.
If we use the communicator MPI.COMM_SELF, each process initialised when running the script would have a version of the full mesh local to its process.
Creating a mesh on each process#
local_domain = mesh.create_rectangle(MPI.COMM_SELF, extent, [Nx, Ny], mesh.CellType.quadrilateral)
We plot the mesh.
With Pyvista, we can export the plots to many formats including pngs, interactive notebook plots, and html
plotter.view_xy()
plotter.camera.zoom(2)
plotter.export_html("./beam.html")
Setting up a variational problem#
We will solve the heat equation, with a backward Euler time stepping scheme, ie
with \(u_D = y\cos(0.25t)\), \(f=0\). For this example, we take \(\Omega\) to be rectangle defined above, \(\Omega_\text{D}\) if the left-hand edge of the rectangle, and \(\Omega_\text{N}\) is the remaining three edges of the rectangle.
We start by defining the function space, the corresponding test and trial functions, as well as material and temporal parameters. Note that we use explicit imports from UFL to create the test and trial functions, to avoid confusion as to where they originate from. DOLFINx and UFL support both real and complex valued functions. However, to be able to use the PETSc linear algebra backend, which only supports a single floating type at compilation, we need to use appropriate scalar types in our variational form. This ensures that we generate consistent matrices and vectors.
from ufl import (
SpatialCoordinate,
TestFunction,
TrialFunction,
as_vector,
dx,
grad,
inner,
system,
)
V = fem.functionspace(domain, ("Lagrange", 1))
u = TrialFunction(V)
v = TestFunction(V)
un = fem.Function(V)
f = fem.Constant(domain, 0.0)
mu = fem.Constant(domain, 2.3)
dt = fem.Constant(domain, 0.05)
The variational form can be written in UFL syntax, as done in legacy DOLFIN:
Creating Dirichlet boundary conditions#
Creating a time dependent boundary condition#
There are many ways of creating boundary conditions. In this example, we will create function \(u_\text{D}(x,t)\) dependent on both space and time. To do this, we define a function that takes a 2-dimensional array x. Each column of x corresponds to an input coordinate \((x,y,z)\) and this function operates directly on the columns of x.
import numpy as np
def uD_function(t):
return lambda x: x[1] * np.cos(0.25 * t)
uD = fem.Function(V)
t = 0
uD.interpolate(uD_function(t))
To give the user freedom to set boundary conditions on single degrees of freedom, the function dolfinx.fem.dirichletbc() takes in the list of degrees of freedom (DOFs) as input.
The DOFs on the boundary can be obtained in many ways: DOLFINx supplies a few convenience functions, such as dolfinx.fem.locate_dofs_topological() and dolfinx.fem.locate_dofs_geometrical().
Locating dofs topologically is generally advised, as certain finite elements have DOFs that do not have a geometrical coordinates associated with them (eg Nédélec and Raviart–Thomas).
DOLFINx also has convenicence functions to obtain a list of all boundary facets.
def dirichlet_facets(x):
return np.isclose(x[0], length)
tdim = domain.topology.dim
bc_facets = mesh.locate_entities_boundary(domain, tdim - 1, dirichlet_facets)
bndry_dofs = fem.locate_dofs_topological(V, tdim - 1, bc_facets)
bcs = [fem.dirichletbc(uD, bndry_dofs)]
Setting up a time dependent solver#
As the left hand side of our problem (the matrix) is time independent, we would like avoid re-assembling it at every time step. DOLFINx gives the user more control over assembly so that this can be done. We assemble the matrix once outside the temporal loop.
import dolfinx.fem.petsc as petsc
compiled_a = fem.form(a)
A = petsc.assemble_matrix(compiled_a, bcs=bcs)
A.assemble()
Next, we can generate the integration kernel for the right hand side (RHS), and create the RHS vector b that we will assemble into at each time step.
compiled_L = fem.form(L)
b = fem.Function(V)
We next create the PETSc KSP (Krylov subspace method) solver, and set it to solve using an algebraic multigrid method.
from petsc4py import PETSc
solver = PETSc.KSP().create(domain.comm)
solver.setOperators(A)
solver.setType(PETSc.KSP.Type.CG)
pc = solver.getPC()
pc.setType(PETSc.PC.Type.HYPRE)
pc.setHYPREType("boomeramg")
Plotting a time dependent problem#
As we are solving a time dependent problem, we would like to create a time dependent animation of the solution.
We do this by using pyvista, which uses VTK structures for plotting.
In DOLFINx, we have the convenience function dolfinx.plot.vtk_mesh() that can create meshes compatible with VTK formatting, based on meshes of (discontinuous) Lagrange function spaces.
topology, cells, geometry = plot.vtk_mesh(V)
uh = fem.Function(V)
grid = pyvista.UnstructuredGrid(topology, cells, geometry)
grid.point_data["uh"] = uh.x.array
viridis = mpl.colormaps["viridis"]
sargs = dict(
title_font_size=25,
label_font_size=20,
fmt="%.2e",
color="black",
position_x=0.1,
position_y=0.8,
width=0.8,
height=0.1,
)
renderer = plotter.add_mesh(
grid,
show_edges=True,
lighting=False,
cmap=viridis,
scalar_bar_args=sargs,
clim=[0, height],
)
plotter.view_xy()
plotter.camera.zoom(1.3)
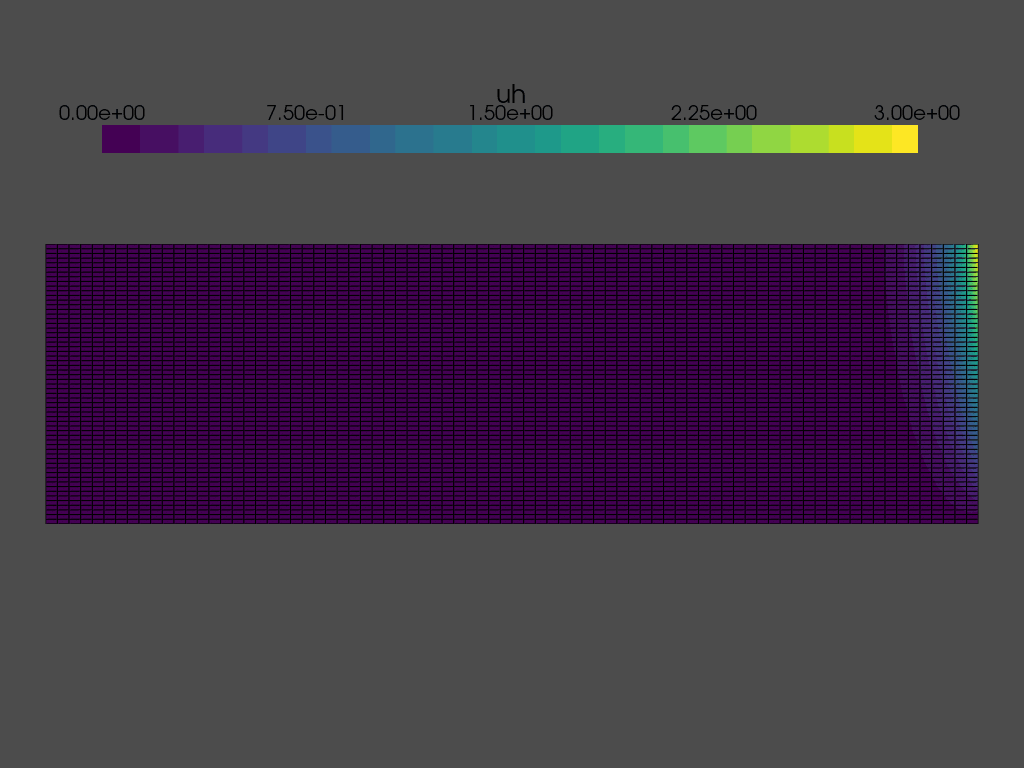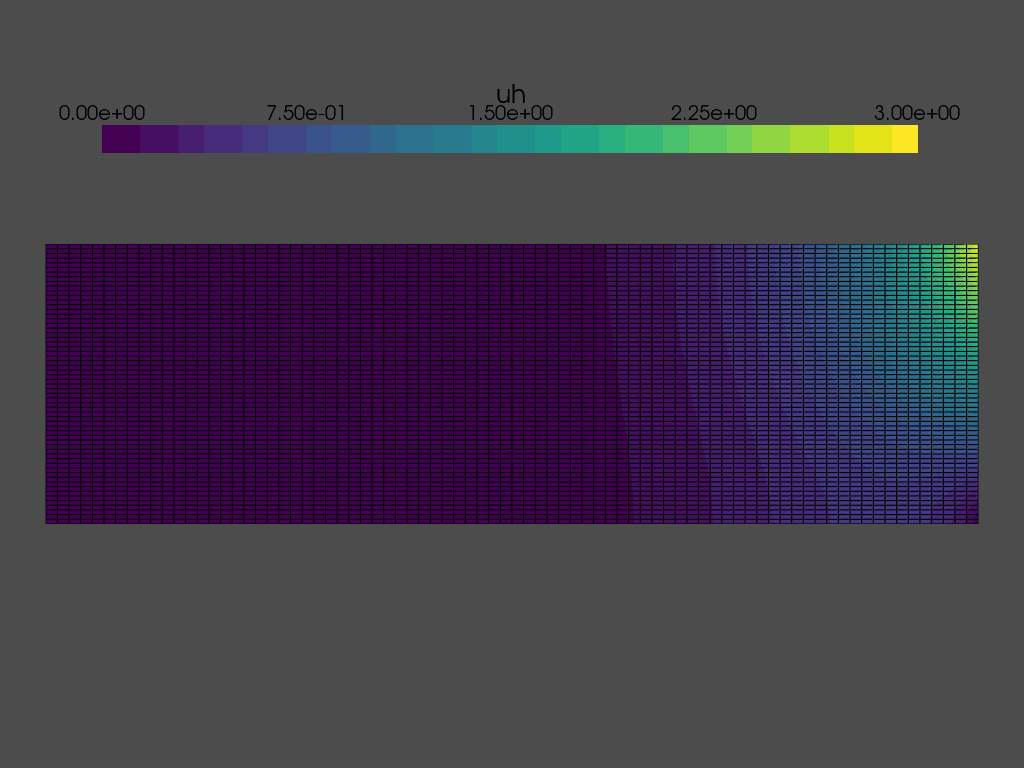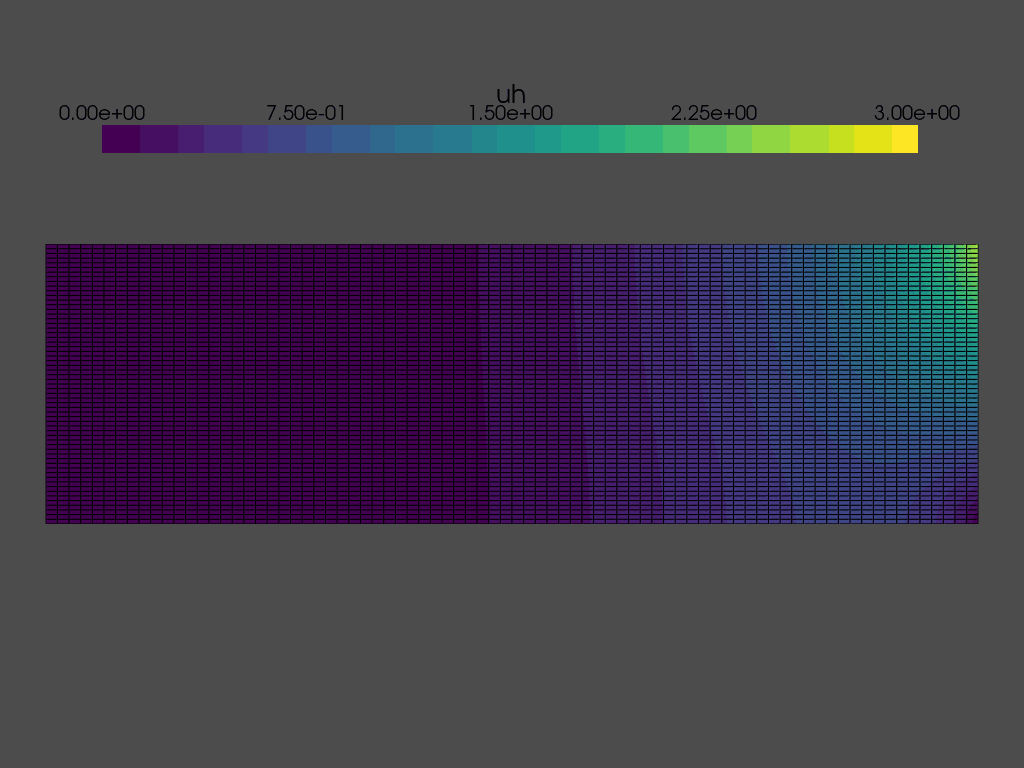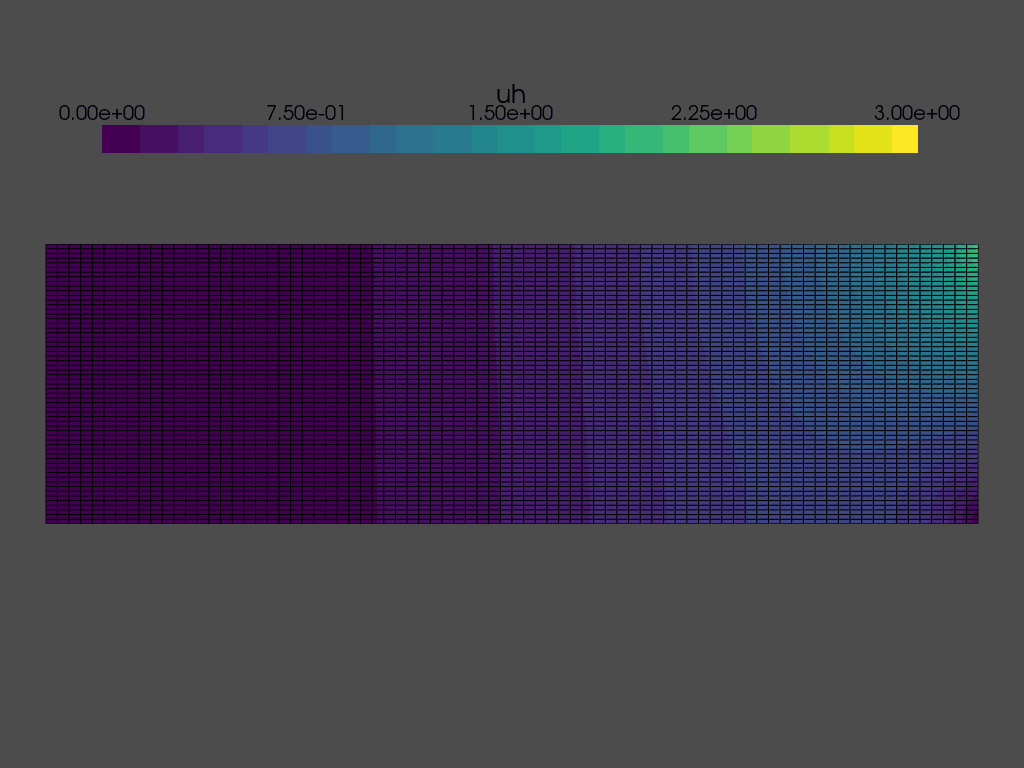
Solving a time dependent problem#
We are now ready to solve the time dependent problem. At each time step, we need to:
Update the time dependent boundary condition and source
Reassemble the right hand side vector
bApply boundary conditions to
bSolve linear problem
Au = bUpdate previous time step,
un = u
T = np.pi
while t < T:
# Update boundary condition
t += dt.value
uD.interpolate(uD_function(t))
# Assemble RHS
b.x.array[:] = 0
petsc.assemble_vector(b.x.petsc_vec, compiled_L)
# Apply boundary condition
petsc.apply_lifting(b.x.petsc_vec, [compiled_a], [bcs])
b.x.scatter_reverse(la.InsertMode.add)
fem.petsc.set_bc(b.x.petsc_vec, bcs)
# Solve linear problem
solver.solve(b.x.petsc_vec, uh.x.petsc_vec)
uh.x.scatter_forward()
# Update un
un.x.array[:] = uh.x.array
# Update plotter
grid.point_data["uh"][:] = uh.x.array
plotter.write_frame()
Post-processing without projections#
In legacy dolfin, the only way of post-processing a ufl-expression over the domain, would be by using a projection.
This would not be scalable in most cases.
Therefore, we have introduced dolfinx.fem.Expression, which can be used to evaluate a ufl expression
at any given (reference) point in any cell (local to process). Let us consider
W = fem.functionspace(domain, ("DQ", 1))
expr = fem.Expression(x_grad, W.element.interpolation_points)
w = fem.Function(W)
w.interpolate(expr)
