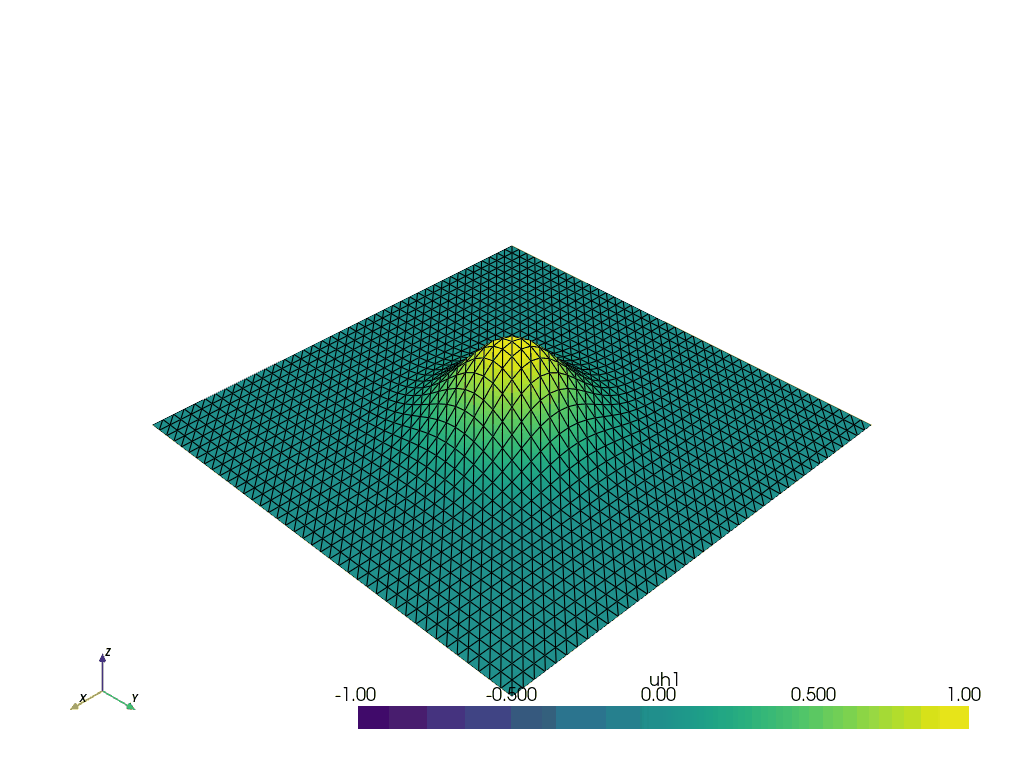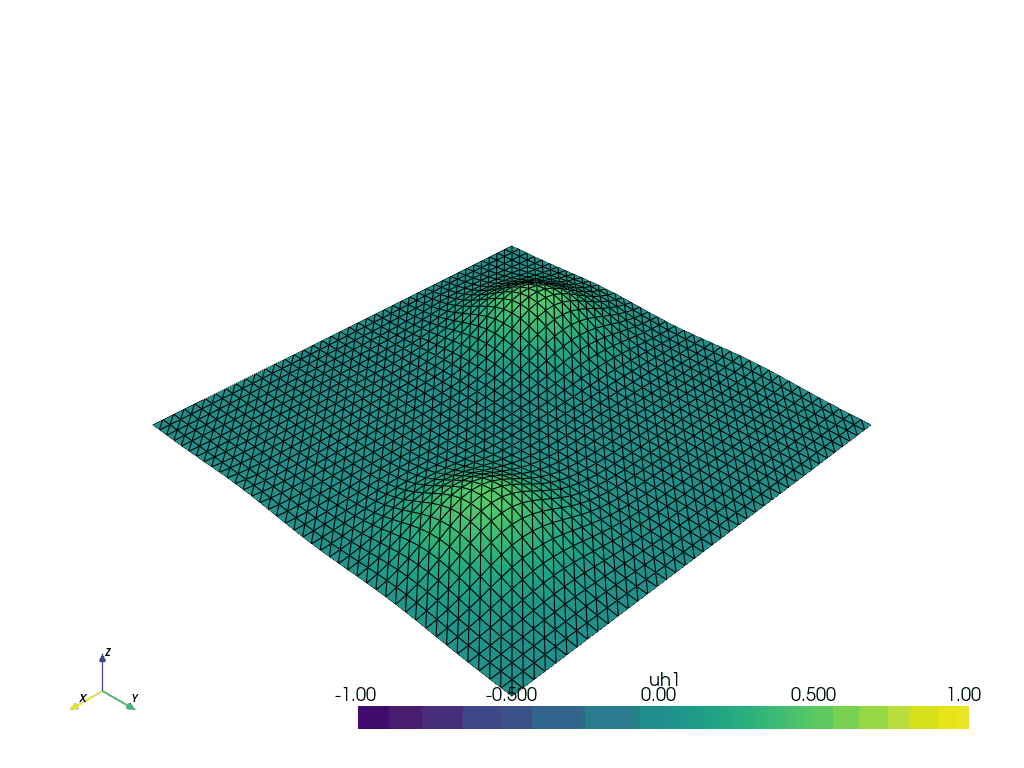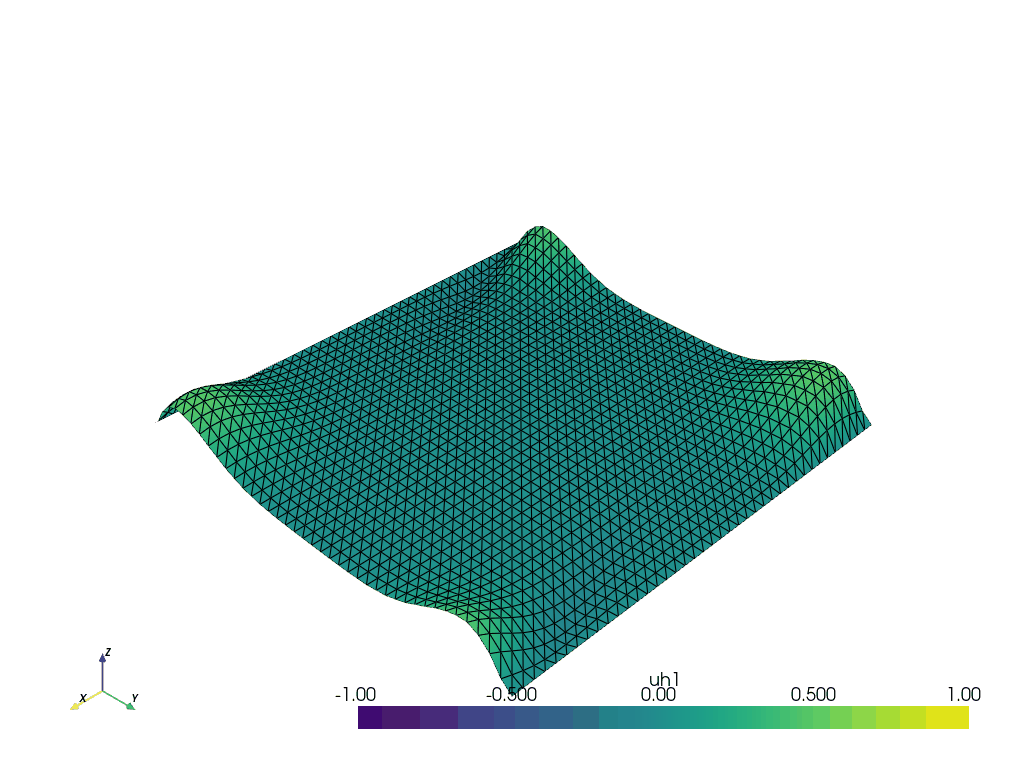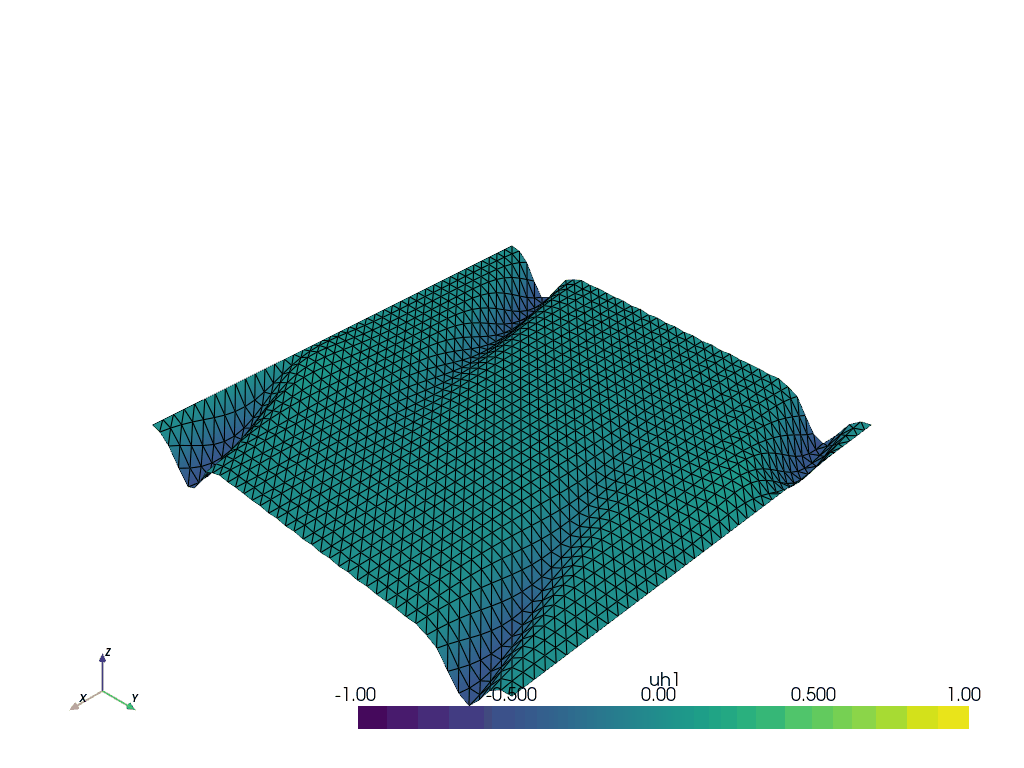
Anisotropic wave system with periodic boundary conditions

Anisotropic wave system with periodic boundary conditions#

Author Jørgen S. Dokken and Markus Renoldner

License MIT

This demo illustrates how to use the MPC package to enforce periodic boundary conditions for a linear wave problem.

Mathematical formulation#

We want to compute two time-dependent functions \((u,\phi)\) on the unitsquare \(\Omega=(0,1)^2\), that solve

\[\begin{split} \begin{cases} \displaystyle \partial_{t} u + b\cdot \nabla \phi=0, \\ \partial_{t} \phi + b\cdot \nabla u=0, \end{cases} \end{split}\]

where the given vectorfield satisfies \((\operatorname{div} b = 0)\), that dictates the advection direction, and \((f,g)\) are given functions.

Smooth solutions of the above system also satisfy a decoupled version of the above system,

\[ \partial_{tt} u + b\cdot\nabla (b\cdot\nabla u) = 0. \]

This last problem resembles the linear wave equation, which explains the wavey dynamics of the solution.

The aim of this tutorial is to show how to use periodic boundary conditions. We will choose the following setting:

\[\begin{split} \begin{align*} \phi|_{\Gamma_D} &=0 , \\ \phi|_{\Gamma_l} &= \phi|_{\Gamma_r}, \\ u|_{\Gamma_l} &= |_{\Gamma_r}, \end{align*} \end{split}\]

where we set \((\partial\Omega = \Gamma_D\cup \Gamma_l \cup \Gamma_r)\), with

\[\begin{split} \begin{align*} \Gamma_D &:=\{(x,y)\in \bar{\Omega}: y=0 \text{ or }y=1\},\quad&&\text{i.e. the bottom and top wall}\\ \Gamma_l &:=\{(x,y)\in \bar{\Omega}: x=0\},\quad&&\text{i.e. the left wall}\\ \Gamma_r &:=\{(x,y)\in \bar{\Omega}: x=1\},\quad&&\text{i.e. the right wall}. \end{align*} \end{split}\]

We start by the various modules required for this demo

import typing

from mpi4py import MPI
from petsc4py import PETSc

import dolfinx.fem as fem
import dolfinx.la.petsc
import numpy as np
import pyvista
from basix.ufl import element
from dolfinx import default_scalar_type, plot
from dolfinx.fem import Constant, Function, assemble_scalar, form, functionspace
from dolfinx.mesh import create_unit_square, locate_entities_boundary
from ufl import (
    FacetNormal,
    MixedFunctionSpace,
    SpatialCoordinate,
    TestFunctions,
    TrialFunctions,
    dx,
    extract_blocks,
    grad,
    inner,
)

from dolfinx_mpc import (
    MultiPointConstraint,
    apply_lifting,
    assemble_matrix_nest,
    assemble_vector_nest,
    create_matrix_nest,
    create_vector_nest,
)

Next, we create some convenience functions to create a gif from a given function

def create_gif(
    plotfunc: dolfinx.fem.Function, filename: str, fps: float
) -> tuple[pyvista.UnstructuredGrid, pyvista.Plotter]:
    """
    Create a GIF animation from a given plotting function and function space.

    Args:
        plotfunc: The plotting function that generates the data to be visualized.
        filename: The name of the output GIF file.
        fps: Frames per second for the GIF animation.
    Returns:
        tuple: A tuple containing the grid and plotter used for creating the GIF.

    Example:

        .. code-block:: python

            grid, plotter = create_gif(plotfunc, "output.gif", 10)

            for i in range(N):
                plotter = update_gif(...)
            finalize_gif(...)
    """
    grid = pyvista.UnstructuredGrid(*plot.vtk_mesh(plotfunc.function_space))
    plotter = pyvista.Plotter(off_screen=True)

    plotter.open_gif(filename, fps=fps)
    plotter.show_axes()  # type: ignore[call-arg]
    grid.point_data["uh1"] = plotfunc.x.array

    return grid, plotter


def update_gif(
    grid: pyvista.UnstructuredGrid,
    plotter: pyvista.Plotter,
    plotfunc: dolfinx.fem.Function,
    warp_gif: bool,
    clip_gif: bool,
    clip_normal: typing.Literal["x", "y", "z", "-x", "-y", "-z"] = "y",
):
    """
    Update the plotter with the given grid and plot function, and optionally warp or clip the grid.

    Args:
        grid: The grid to be plotted.
        plotter: The plotter instance used for plotting.
        plotfunc: An object containing the data to be plotted, with an attribute `x.array`.
        warp_gif: If True, warp the grid by the scalar values.
        clip_gif: If True, clip the grid along the specified normal.
        clip_normal: The normal direction for clipping. Default is "y".

    Returns:
    pyvista.Plotter: The updated plotter instance.
    """
    maxval = max(plotfunc.x.array)
    maxval = 1
    grid.point_data["uh"] = plotfunc.x.array

    if warp_gif and clip_gif:
        PETSc.Sys.Print("warp and clip not possible at the same time")  # type: ignore
        plotter.clear()
        plotter.add_mesh(grid, clim=[-maxval, maxval], show_edges=True)
    elif warp_gif:
        grid_warped = grid.warp_by_scalar("uh", factor=0.2 * 1 / maxval)
        plotter.clear()
        plotter.add_mesh(grid_warped, clim=[-maxval, maxval], show_edges=True)
    elif clip_gif:
        grad_clipped = grid.clip(clip_normal, invert=True)
        plotter.clear()
        plotter.add_mesh(grad_clipped, clim=[-maxval, maxval], show_edges=True)
        plotter.add_mesh(grid, style="wireframe", clim=[-maxval, maxval], show_edges=True)
    else:
        plotter.clear()
        plotter.add_mesh(grid, clim=[-maxval, maxval], show_edges=True)

    plotter.write_frame()
    plotter.show_axes()  # type: ignore[call-arg]
    return plotter


def finalize_gif(plotter: pyvista.Plotter):
    plotter.close()

The goal is to solve the wave system using Lagrange Finite Elements. For this we propose the following weak formulation:

\[\begin{split} \begin{cases} \displaystyle \int_\Omega \partial_{t}u v + \int_\Omega b\cdot\nabla\phi v=0 \quad \forall v \in X^r(\Omega)\\ \displaystyle\int_\Omega \partial_{t} \phi \psi - \int_\Omega u b\cdot\nabla\psi = 0 \quad \forall \psi\in X^r_0(\Omega) \end{cases} \end{split}\]

Here \((X^r)\) denotes the Lagrange order \((r)\), global FEM space of piecewise polynomial functions that are globally continuous, defined as

\[ X^r(\Omega) := \{u_h \in C (\bar{\Omega} ) : u_h |_K \in \mathbb{P}^r\ \forall K\} . \]

The notation \((X^r_0)\) denotes the restriction of the above space to a space with zero boundary values.

For the derivative in time, we use the Crank-Nicolson scheme. We define some matrices:

\[\begin{split} \begin{aligned} M_{ij} &= \left \langle v_j, v_i \right \rangle \\ N_{ij} &= \left \langle \psi_j,\psi_i \right \rangle \\ E_{ij} &= \left \langle \nabla\psi_j , b v_i \right \rangle \\ F_{ij} &= \left \langle v_j b,\nabla \psi_i\right \rangle \end{aligned} \end{split}\]

The scheme is then:

\[\begin{split} \begin{aligned} \begin{pmatrix} M & + \frac{\Delta t}{2}E \\ - \frac{\Delta t}{2}F & N \end{pmatrix} \begin{pmatrix} \vec u ^{n+1}\\ \vec\phi^{n+1} \end{pmatrix} = \begin{pmatrix} M \vec u^n - \frac{\Delta t}{2} E \vec\phi^n\\ \frac{\Delta t}{2} F\vec u^n +N\vec \phi^n \end{pmatrix} \end{aligned} \end{split}\]

It turns out the continuous problem, as well as the fully discrete version is stable, and one can show, that solutions \((u,\phi)\) conserve the energy

\[\mathcal{E} := \int_\Omega u^2 +\phi^2.\]

We will now implement this problem in fenicsx.

dt = 0.02  # time step
t = 0.0  # initial time
T_end = 1  # final time
num_steps = int(T_end / dt)  # number of time steps
Nx = 40  # number of elements in x and y direction
h = 1 / Nx  # mesh size
bconst = 1.0  # magnitude of the advection field

if MPI.COMM_WORLD.size == 1:
    filename_gifV = "testV.gif"
    filename_gifp = "testp.gif"
else:
    filename_gifV = f"testV_{MPI.COMM_WORLD.rank}.gif"
    filename_gifp = f"testp_{MPI.COMM_WORLD.rank}.gif"

warp_gif = True

Mesh, spaces, functions#

We create a ufl.MixedFunctionSpace for the functions V,p

msh = create_unit_square(MPI.COMM_WORLD, Nx, Nx)
P1 = element("Lagrange", "triangle", 1)
XV = functionspace(msh, P1)
Xp = functionspace(msh, P1)
Z = MixedFunctionSpace(XV, Xp)
eps = 0.8
bfield = Constant(msh, (eps, np.sqrt(1 - eps**2)))
x = SpatialCoordinate(msh)
n = FacetNormal(msh)

Dirichlet BC Along the top and bottom wall, we set `p=0``

facets = locate_entities_boundary(
    msh, dim=1, marker=lambda x: np.logical_or.reduce((np.isclose(x[1], 1.0), np.isclose(x[1], 0.0)))
)
dofs = fem.locate_dofs_topological(V=Xp, entity_dim=1, entities=facets)
bcs = [fem.dirichletbc(np.array(0.0), dofs=dofs, V=Xp)]

Periodic BC#

Along the left and right wall, we set periodic boundary conditions

tol = 250 * np.finfo(default_scalar_type).resolution

We will now identify the set \(\{(x,y) \in \partial \Omega: x=1\}\)

def periodic_boundary(x):
    return np.isclose(x[0], 1, atol=tol)

Now we define the periodic identification of points on the left and right wall This identification is only valid on the periodic boundary

def periodic_relation(x):
    out_x = np.zeros_like(x)
    out_x[0] = 0  # map x=1 to x=0
    out_x[1] = x[1]  # keep y-coord as is
    return out_x

For each of the sapces Xp, XV, we create a dolfinx_mpc.MultiPointConstraint and use create_periodic_constraint_geometrical to create the periodic constraints

mpc_p = MultiPointConstraint(Xp)
mpc_p.create_periodic_constraint_geometrical(Xp, periodic_boundary, periodic_relation, bcs)
mpc_p.finalize()

mpc_V = MultiPointConstraint(XV)
mpc_V.create_periodic_constraint_geometrical(XV, periodic_boundary, periodic_relation, bcs)
mpc_V.finalize()

We can now define the dolfinx.fem.Function for the new time step values, as well as the trial and test functions

Note

Note that we use the mpc.function_space as input for the functions.

# new time step values
V_new = fem.Function(mpc_V.function_space)
p_new = fem.Function(mpc_p.function_space)
V, p = TrialFunctions(Z)
W, q = TestFunctions(Z)

# initial conditions
V_old = Function(mpc_V.function_space)
p_old = Function(mpc_p.function_space)
V_old.interpolate(lambda x: 0.0 * x[0])
p_old.interpolate(lambda x: np.exp(-1 * (((x[0] - 0.5) / 0.15) ** 2 + ((x[1] - 0.5) / 0.15) ** 2)))

We set up the gifs using the convenience function defined above

gridV, plotterV = create_gif(V_old, filename_gifV, fps=0.1 / dt)
gridp, plotterp = create_gif(p_old, filename_gifp, fps=0.1 / dt)

2025-10-22 11:02:51.589 (   0.951s) [    7F2EEE76B080]vtkXOpenGLRenderWindow.:1458  WARN| bad X server connection. DISPLAY=

We define the weak form of the left hand side and use extract_blocks to extract the block structure of the bilinear form.

M = inner(V, W) * dx
E = inner(grad(p), bfield * W) * dx
F = inner(grad(V), bfield * q) * dx
N = inner(p, q) * dx
a = M + dt / 2 * E + dt / 2 * F + N
a_blocked = form(extract_blocks(a))

As the system matrix is time-independent, we use create_matrix_nest to create the system matrix, and assemble_matrix_nest to assemble the matrix once, outside the temporal loop.

A = create_matrix_nest(a_blocked, [mpc_V, mpc_p])
assemble_matrix_nest(A, a_blocked, [mpc_V, mpc_p], bcs)
A.assemble()

We define the Krylov subspace solver using petsc4py.PETSc.KSP and use a direct LU solver as preconditioner.

solver = PETSc.KSP().create(msh.comm)  # type: ignore
solver.setOperators(A)
solver.setType(PETSc.KSP.Type.PREONLY)  # type: ignore
solver.getPC().setType(PETSc.PC.Type.LU)  # type: ignore

As we did for the bilinear form, we define the linear form, extract the block structure, and create the petsc4py.PETSc.Vec that we will assemble into at each time step.

L = (
    inner(V_old, W) * dx
    - dt / 2 * inner(grad(p_old), bfield * W) * dx
    + inner(p_old, q) * dx
    - dt / 2 * inner(grad(V_old), bfield * q) * dx
)
L_blocked = form(extract_blocks(L))
b = create_vector_nest(L_blocked, [mpc_V, mpc_p])

We perform the time dependent solve in a temporal loop. Note that we use assemble_vector_nest, apply_lifting, and backsubstitution to handle the periodic conditions.

progress_0 = 0
for i in range(num_steps):
    t += dt

    # update RHS
    assemble_vector_nest(b, L_blocked, [mpc_V, mpc_p])

    # Dirichlet BC values in RHS
    apply_lifting(b, a_blocked, bcs, [mpc_V, mpc_p])
    dolfinx.la.petsc._ghost_update(
        b,
        insert_mode=PETSc.InsertMode.ADD_VALUES,  # type: ignore
        scatter_mode=PETSc.ScatterMode.REVERSE,  # type: ignore
    )
    bcs0 = fem.bcs_by_block(fem.extract_function_spaces(L_blocked), bcs)
    fem.petsc.set_bc(b, bcs0)

    # solve
    Vp_vec = b.copy()
    solver.solve(b, Vp_vec)
    dolfinx.la.petsc._ghost_update(
        Vp_vec,
        insert_mode=PETSc.InsertMode.INSERT,  # type: ignore
        scatter_mode=PETSc.ScatterMode.FORWARD,  # type: ignore
    )  # type: ignore
    dolfinx.fem.petsc.assign(Vp_vec, [V_new, p_new])

    # update MPC slave dofs
    mpc_V.backsubstitution(V_new)
    mpc_p.backsubstitution(p_new)

    # progress
    progress = int(((i + 1) / num_steps) * 100)
    if progress >= progress_0 + 20:
        progress_0 = progress
        E_local = assemble_scalar(form(inner(V_new, V_new) * dx + inner(p_new, p_new) * dx))
        E = msh.comm.allreduce(E_local, op=MPI.SUM)
        PETSc.Sys.Print(f"|--progress: {progress}% \t time: {t:6.5f} \t {E=:.15e}:")  # type: ignore

    # Update solution at previous time step
    V_old.x.array[:] = V_new.x.array
    p_old.x.array[:] = p_new.x.array

    # gif
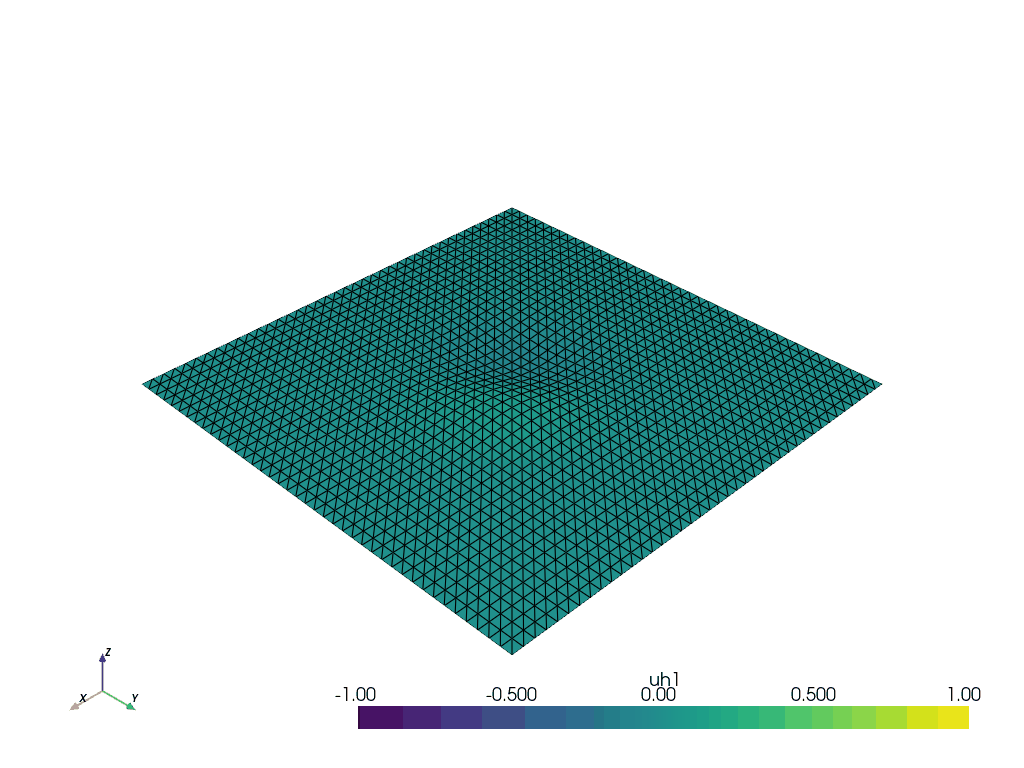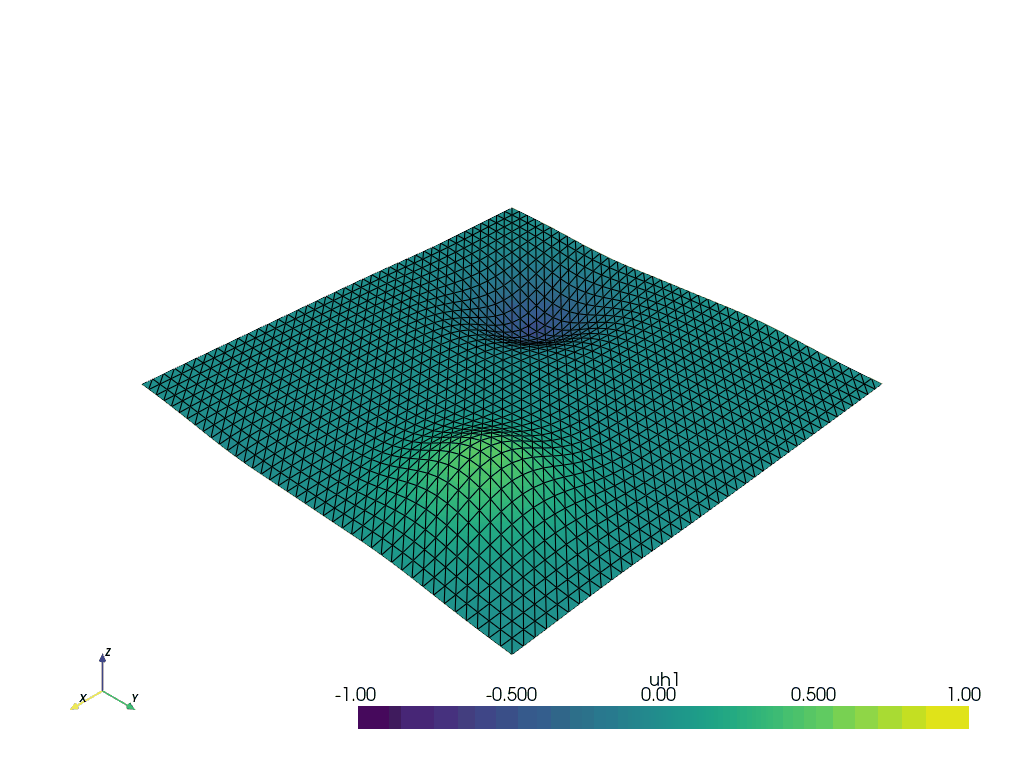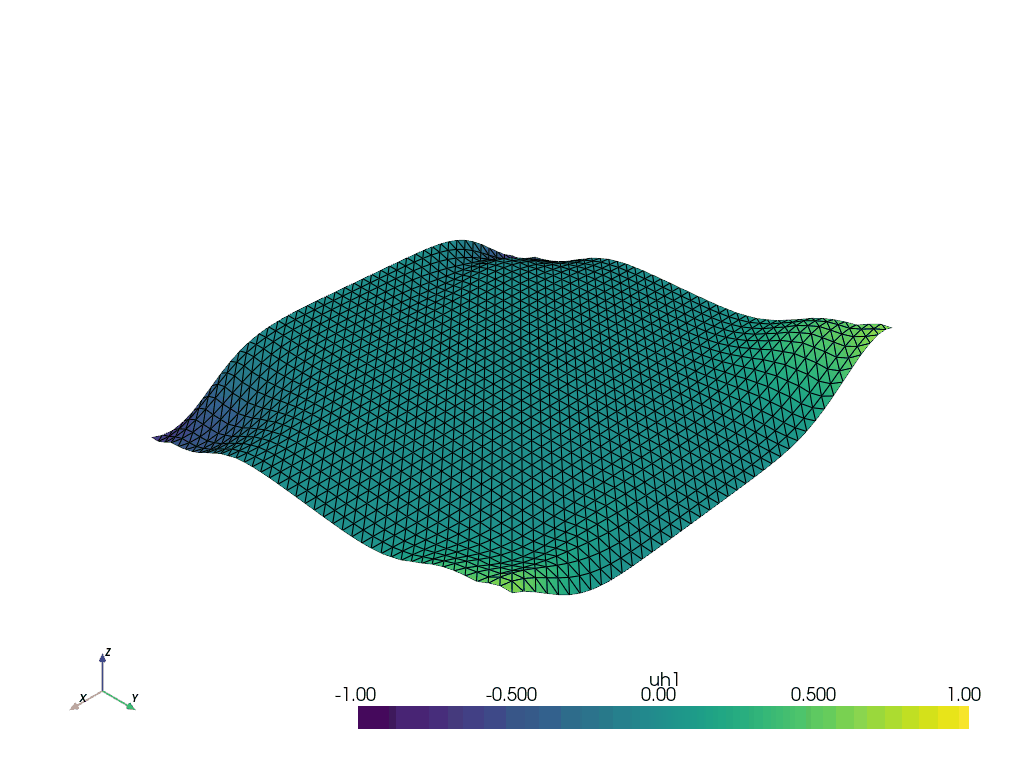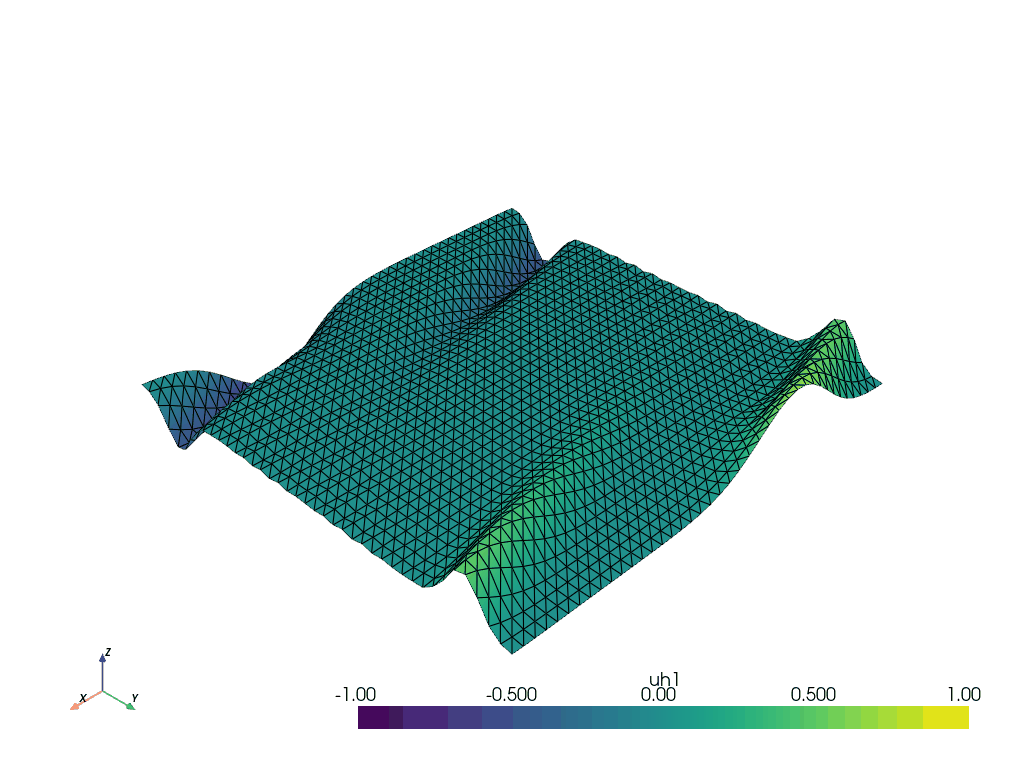
    plotterV = update_gif(gridV, plotterV, V_old, warp_gif, clip_gif=False)
    plotterp = update_gif(gridp, plotterp, p_old, warp_gif, clip_gif=False)

solver.destroy()
b.destroy()
Vp_vec.destroy()

|--progress: 20% 	 time: 0.20000 	 E=3.501905082164686e-02:

|--progress: 40% 	 time: 0.40000 	 E=3.501905082164699e-02:

|--progress: 60% 	 time: 0.60000 	 E=3.501905082164716e-02:

|--progress: 80% 	 time: 0.80000 	 E=3.501905082164716e-02:

|--progress: 100% 	 time: 1.00000 	 E=3.501905082164725e-02:

<petsc4py.PETSc.Vec at 0x7f2e751a8180>

We store the GIF to file

finalize_gif(plotterV)
finalize_gif(plotterp)
PETSc.Sys.Print(f"gifs saved as {filename_gifV}, {filename_gifp}")  # type: ignore

gifs saved as testV.gif, testp.gif
gifV gifp
Contents