Function and expression evaluation

Function and expression evaluation#

In this section, we will look at how we can extract data once we have solved our variational problem. To make this section concise, we will use functions with expressions that are already defined (not through a PDE), but through interpolation.

We start by creating a 3D mesh

from mpi4py import MPI
import dolfinx
import numpy as np

N = 2
mesh = dolfinx.mesh.create_box(
    MPI.COMM_WORLD,
    [np.array([0, 0, 0]), np.array([2, 1.3, 0.8])],
    [N, N, N],
    dolfinx.mesh.CellType.tetrahedron,
    ghost_mode=dolfinx.mesh.GhostMode.shared_facet,
)

We start by considering a scalar function in a discontinuous space

V = dolfinx.fem.functionspace(mesh, ("DG", 2))
u = dolfinx.fem.Function(V)

Interpolation on a subset of cells#

We would like to interpolate the function

\[\begin{split} \begin{align} u = \begin{cases} x[0]^2 & \text{if } x[0] < 1\\ x[1] & \text{otherwise} \end{cases} \end{align} \end{split}\]

We start by locating the cells that satisfies this condition. In Locating a subset of entities on a boundary we learnt how to use dolfinx.mesh.locate_entities_boundary to locate entites. In this section we will use dolfinx.mesh.locate_entities which does the same, but for all entities in the mesh.

tdim = mesh.topology.dim
left_cells = dolfinx.mesh.locate_entities(mesh, tdim, lambda x: x[0] <= 1 + 1e-14)
right_cells = dolfinx.mesh.locate_entities(mesh, tdim, lambda x: x[0] >= 1 - 1e-14)

We can now interpolate the function onto each of these subsets

u.interpolate(lambda x: x[0] ** 2, cells0=left_cells)
u.interpolate(lambda x: x[1], cells0=right_cells)

Whenever we interpolate on sub-sets of cells, we need to scatter forward the values

u.x.scatter_forward()

Evalation at a point#

We want to evaluate the function at a point in the mesh that does not align with the nodes of the mesh. We do this through a sequence of steps:

As the mesh will be distributed on multiple processes, we have to determine which processes that has the point.
Then, for the processes that has the point, we need to figure out what cell the point is in.
Finally, we push this point back to the reference element, so that we can evaluate the basis functions, combine them with the coefficients on the given cell and push them forward to the physical space.

Step 1: Determine which processes that has the cell#

As looping through all the cells, and compute exact collisions is expensive, we accelerate the search by using an axis-aligned bounding box tree. This is a tree that recursively divides the mesh into smaller and smaller boxes, such that we can quickly search through the tree to find the cells that might contain the point of interest.

bb_tree = dolfinx.geometry.bb_tree(mesh, mesh.topology.dim)

Note

Bounding boxes of other entities As seen below, we send in the topological dimension of the entities that we are interested in. This means that you can make a bounding box tree for facets, edges or vertices as well if it is needed.

Bounding boxes of subsets of entities

In many scenarios, we already have a notion about which entities we are interested in, we can create a bounding box tree of only these entities by sending in the entities as a list.

sub_bb_tree = dolfinx.geometry.bb_tree(mesh, mesh.topology.dim, left_cells)

We can now send the points into dolfinx.geometry.compute_collisions_point to find the cells that contain the point.

Point collision in parallel

Note that each bounding box tree is local to the given process, and thus we can send in the same point to all processs, or unique points for each process.

points = np.array([[0.51, 0.32, 0], [1.3, 0.834, 0]], dtype=mesh.geometry.x.dtype)
potential_colliding_cells = dolfinx.geometry.compute_collisions_points(bb_tree, points)

potential_colliding_cells=<AdjacencyList> with 2 nodes
  0: [25 13 17 10 21 29 ]
  1: [4 14 8 16 22 9 ]

Output of compute point collisions

As we observe above, we get an AdjacencyList out of the function compute_collisions_points. This is a list of lists, where the \(ith\) list contains the indices of the cells that has bounding boxes that collide with the \(i\)th point.

potential_colliding_cells.links(0)=array([25, 13, 17, 10, 21, 29], dtype=int32)

Step 2: Determine what cells the point is in#

Now that we have a reduced number of cells to more carefully examine, we can use the Gilbert–Johnson–Keerthi distance algorithm GJK. To find the cells whose convex hull contains the point.

Higher order meshes

As the GJK algorithm work on convex hulls, it is not 100 % accurate for higher order geometries (i.e. coordinate element is higher order, and the facets are curved). However, it is usually a sufficiently good enough approximation to be used in practice. For a more accurate algorithm, one could take all the points that satisfies the boundary box collision, pull them back to the reference element, and check that the resulting coordinate are inside the reference element. However, for non-affine grids this involves solving a non-linear problem (with a Newton type method).

To do this efficiently, we use dolfinx.geometry.compute_colliding_cells which takes in the output of compute_collisions_points and the points.

colliding_cells = dolfinx.geometry.compute_colliding_cells(mesh, potential_colliding_cells, points)

colliding_cells=<AdjacencyList> with 2 nodes
  0: [10 ]
  1: [8 ]

If a point is on an interface between two cells, we can get multiple cells that contain the point. Now, to prepare for step 3, we reduce the set of points and cells to those that are colliding on the current process.

points_on_proc = []
cells = []
for i, point in enumerate(points):
    if len(colliding_cells.links(i)) > 0:
        points_on_proc.append(point)
        cells.append(colliding_cells.links(i)[0])

Step 3: Evaluate function at a point in the cell#

We now have on step left, which is to evaluate the function at the point in the cell. As we saw above, this step involves quite a few operations. Thankfully, these are all encapsulated in the function dolfinx.fem.Function.eval.

points_on_proc = np.array(points_on_proc, dtype=np.float64).reshape(-1, 3)
cells = np.array(cells, dtype=np.int32)
u_values = u.eval(points_on_proc, cells)

points_on_proc=array([[0.51 , 0.32 , 0.   ],
       [1.3  , 0.834, 0.   ]])
u_values=array([[0.2601],
       [0.834 ]])

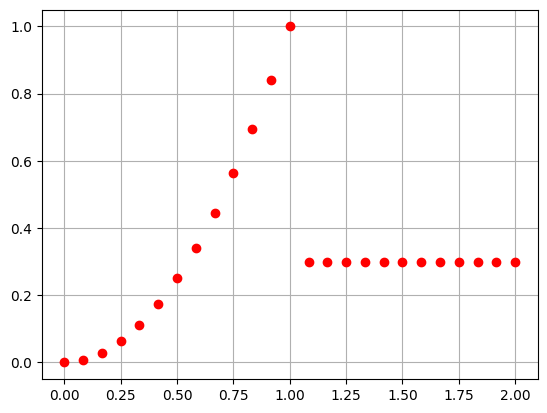
Evaluating along a line \(y=0.3, z=0.2\) and plot the result

Expand the dropdowns below to see the solution

Evaluate a UFL expression#

As we have seen in Generating code for assembling tensors we can generate code for evaluating integrals. We can also non-integrated UFL expressions at any point in the mesh. For this part of the tutorial, we will consider a blocked Lagrange space, with 3 components.

mesh = dolfinx.mesh.create_unit_cube(MPI.COMM_WORLD, 5, 5, 5, dolfinx.cpp.mesh.CellType.hexahedron)
V = dolfinx.fem.functionspace(mesh, ("Lagrange", 2, (3,)))
u = dolfinx.fem.Function(V)

def f(mod, x):
    return x[2] ** 2, x[0] + x[1], x[1] * x[2]

u.interpolate(lambda x: f(np, x))

We will consider

\[ \nabla \times \mathbf{u}=\left( \frac{\partial u_2}{\partial x_1} - \frac{\partial u_1}{\partial x_2}, \frac{\partial u_0}{\partial x_2} - \frac{\partial u_2}{\partial x_0}, \frac{\partial u_1}{\partial x_0} - \frac{\partial u_0}{\partial x_1} \right) \]

We can write this in UFL as

import ufl

curl_u = ufl.curl(u)

We can use dolfinx.fem.Expression to compile the evaluation of this expression at a set of points in the reference element. For instance, we can choose the point \((0.2, 0.3, 0.5)\) which is in the reference hexahedron.

points = np.array([[0.2, 0.3, 0.5]], dtype=np.float64)
expr = dolfinx.fem.Expression(curl_u, points)

We can now evaluate the expression at this point in any cell in the mesh We pick two random cells on the process

num_cells_local = mesh.topology.index_map(mesh.topology.dim).size_local
cells = np.random.randint(0, num_cells_local, 2, dtype=np.int32)
values = expr.eval(mesh, cells)

We can inspect what the coordinates in the physical cell is by using the same strategy of ufl.SpatialCoordinate(mesh)

x_expr = dolfinx.fem.Expression(ufl.SpatialCoordinate(mesh), points)
coords = x_expr.eval(mesh, cells)

values=array([[0.5, 1. , 1. ],
       [0.3, 0.6, 1. ]])
coords=array([[0.84, 0.86, 0.5 ],
       [0.84, 0.26, 0.3 ]])

What points in the reference cells could be interesting to evaluate at?

In theory any point could be interesting to evaluate at, but usually evaluating at a set of quadrature points (for debugging) or at the interpolation points of a finite element.

Interpolation of a UFL expression#

We can for instance interpolate the gradient of a function into another function space. We will be inspired by the De Rahm complex And interpolate the gradient of a \(H^1\) function into \(H^{k-1}(curl)\)

Q = dolfinx.fem.functionspace(mesh, ("Lagrange", 2))
q = dolfinx.fem.Function(Q)

def f(x):
    return x[0] ** 2 + 2 * x[1] ** 2 + x[1] * x[2]

q.interpolate(f)

grad_q = ufl.grad(q)

P = dolfinx.fem.functionspace(mesh, ("N1curl", 2))
p = dolfinx.fem.Function(P)

grad_expr = dolfinx.fem.Expression(grad_q, P.element.interpolation_points())

p.interpolate(grad_expr)

def grad_f(x):
    return (2 * x[0], 4 * x[1] + x[2], x[1])

x = ufl.SpatialCoordinate(mesh)
f_ex = ufl.as_vector(grad_f(x))

L2_error = dolfinx.fem.form(ufl.inner(p - f_ex, p - f_ex) * ufl.dx)
local_error = dolfinx.fem.assemble_scalar(L2_error)
global_error = np.sqrt(mesh.comm.allreduce(local_error, op=MPI.SUM))

global_error=np.float64(2.365361863720135e-14)

Expression evaluation on facets#

Another neat feature for coupling to other codes it that we can evaluate expressions on facets. This could for instance involve the ufl.FacetNormal, which represents the normal point out of any facet of the cell. We can for instance consider the heat flux on the boundary of a domain.

n = ufl.FacetNormal(mesh)
heat_flux = ufl.dot(ufl.grad(q), n)

Integration entities#

Until now, we have represented the different entities of the domain with a given local index. This was the case for both cells, facets, edges and vertices. However, to be able to define the side of a facet we would like to evaluate an expression, we need to associate it with a cell. We do this by looking at all the facets associated with the cell, and then find its local index.

Integration entity

There are three distinct integration entities in FEniCS:

For cell integrals: The cell index itself is the integration entity
For exterior facet integrals: The cell index and the local facet index is the integration entity as a tuple (cell, local_facet)
For interior facet integrals: A tuple consisting of the (cell, local_facet) for both cells connected to the facet, i.e. (cell_0, local_facet_0, cell_1, local_facet_1)

We will illustrate this below, by first finding all facets on one of the boundaries of the mesh

tdim = mesh.topology.dim
set_of_facets = dolfinx.mesh.locate_entities_boundary(mesh, tdim - 1, lambda x: np.isclose(x[1], 1))

Next, we create the appropriate connectivities in the mesh to be able to find the local index

mesh.topology.create_connectivity(tdim - 1, tdim)
f_to_c = mesh.topology.connectivity(tdim - 1, tdim)

mesh.topology.create_connectivity(tdim, tdim - 1)
c_to_f = mesh.topology.connectivity(tdim, tdim - 1)

Next, we loop over all the facets we found and locate it’s local index in the cell it is associated to.

cell_facet_pairs = np.empty((len(set_of_facets), 2), dtype=np.int32)
for i, facet in enumerate(set_of_facets):
    cells = f_to_c.links(facet)
    assert len(cells) == 1, "Cell is connected to more than one facet"
    facets = c_to_f.links(cells[0])
    facet_index = np.flatnonzero(facets == facet)
    assert len(facet_index) == 1, "Facet is not connected to cell"
    cell_facet_pairs[i] = (cells[0], facet_index[0])

cell_facet_pairs=array([[ 30,   4],
       [ 44,   4],
       [ 49,   4],
       [ 65,   4],
       [ 60,   4],
       [ 81,   4],
       [ 69,   4],
       [ 85,   4],
       [ 76,   4],
       [ 95,   4],
       [ 99,   4],
       [ 88,   4],
       [102,   4],
       [ 90,   4],
       [105,   4],
       [109,   4],
       [112,   4],
       [104,   4],
       [114,   4],
       [115,   4],
       [118,   4],
       [120,   4],
       [121,   4],
       [123,   4],
       [124,   4]], dtype=int32)

We can pass these pairs to the dolfinx.fem.Expression to evaluate the heat flux on the boundary of the domain. As before, we can get the coordinates of the points in the physical cell with ufl.SpatialCoordinate(mesh)

facet_midpoint = np.array([[0.5, 0.5]], dtype=np.float64)
facet_x = dolfinx.fem.Expression(ufl.SpatialCoordinate(mesh), facet_midpoint)
heat_flux_expr = dolfinx.fem.Expression(heat_flux, facet_midpoint)

coordinates = facet_x.eval(mesh, cell_facet_pairs.flatten())
flux_values = heat_flux_expr.eval(mesh, cell_facet_pairs.flatten())

coordinate=array([0.1, 1. , 0.1]), flux=array([4.1]) exact_flux=4.1
coordinate=array([0.3, 1. , 0.1]), flux=array([4.1]) exact_flux=4.1
coordinate=array([0.1, 1. , 0.3]), flux=array([4.3]) exact_flux=4.3
coordinate=array([0.3, 1. , 0.3]), flux=array([4.3]) exact_flux=4.3
coordinate=array([0.5, 1. , 0.1]), flux=array([4.1]) exact_flux=4.1
coordinate=array([0.5, 1. , 0.3]), flux=array([4.3]) exact_flux=4.3
coordinate=array([0.1, 1. , 0.5]), flux=array([4.5]) exact_flux=4.5
coordinate=array([0.3, 1. , 0.5]), flux=array([4.5]) exact_flux=4.5
coordinate=array([0.7, 1. , 0.1]), flux=array([4.1]) exact_flux=4.1
coordinate=array([0.7, 1. , 0.3]), flux=array([4.3]) exact_flux=4.3
coordinate=array([0.5, 1. , 0.5]), flux=array([4.5]) exact_flux=4.5
coordinate=array([0.1, 1. , 0.7]), flux=array([4.7]) exact_flux=4.7
coordinate=array([0.3, 1. , 0.7]), flux=array([4.7]) exact_flux=4.7
coordinate=array([0.9, 1. , 0.1]), flux=array([4.1]) exact_flux=4.1
coordinate=array([0.9, 1. , 0.3]), flux=array([4.3]) exact_flux=4.3
coordinate=array([0.7, 1. , 0.5]), flux=array([4.5]) exact_flux=4.5
coordinate=array([0.5, 1. , 0.7]), flux=array([4.7]) exact_flux=4.7
coordinate=array([0.1, 1. , 0.9]), flux=array([4.9]) exact_flux=4.9
coordinate=array([0.3, 1. , 0.9]), flux=array([4.9]) exact_flux=4.9
coordinate=array([0.9, 1. , 0.5]), flux=array([4.5]) exact_flux=4.5
coordinate=array([0.7, 1. , 0.7]), flux=array([4.7]) exact_flux=4.7
coordinate=array([0.5, 1. , 0.9]), flux=array([4.9]) exact_flux=4.9
coordinate=array([0.9, 1. , 0.7]), flux=array([4.7]) exact_flux=4.7
coordinate=array([0.7, 1. , 0.9]), flux=array([4.9]) exact_flux=4.9
coordinate=array([0.9, 1. , 0.9]), flux=array([4.9]) exact_flux=4.9