Diffusion of a Gaussian function

Diffusion of a Gaussian function#

Author: Jørgen S. Dokken

Let us now solve a more interesting problem, namely the diffusion of a Gaussian hill. We take the initial value to be

(26)#\[\begin{align} u_0(x,y)&= e^{-ax^2-ay^2} \end{align}\]

for \(a=5\) on the domain \([-2,2]\times[-2,2]\). For this problem we will use homogeneous Dirichlet boundary conditions (\(u_D=0\)).

The first difference from the previous problem is that we are not using a unit square. We create the rectangular domain with dolfinx.mesh.create_rectangle.

import matplotlib as mpl
import pyvista
import ufl
import numpy as np

from petsc4py import PETSc
from mpi4py import MPI

from dolfinx import fem, mesh, io, plot
from dolfinx.fem.petsc import assemble_vector, assemble_matrix, create_vector, apply_lifting, set_bc

# Define temporal parameters
t = 0  # Start time
T = 1.0  # Final time
num_steps = 50
dt = T / num_steps  # time step size

# Define mesh
nx, ny = 50, 50
domain = mesh.create_rectangle(MPI.COMM_WORLD, [np.array([-2, -2]), np.array([2, 2])],
                               [nx, ny], mesh.CellType.triangle)
V = fem.functionspace(domain, ("Lagrange", 1))

Note that we have used a much higher resolution than before to better resolve features of the solution. We also easily update the intial and boundary conditions. Instead of using a class to define the initial condition, we simply use a function

# Create initial condition
def initial_condition(x, a=5):
    return np.exp(-a * (x[0]**2 + x[1]**2))


u_n = fem.Function(V)
u_n.name = "u_n"
u_n.interpolate(initial_condition)

# Create boundary condition
fdim = domain.topology.dim - 1
boundary_facets = mesh.locate_entities_boundary(
    domain, fdim, lambda x: np.full(x.shape[1], True, dtype=bool))
bc = fem.dirichletbc(PETSc.ScalarType(0), fem.locate_dofs_topological(V, fdim, boundary_facets), V)

Time-dependent output#

To visualize the solution in an external program such as Paraview, we create a an XDMFFile which we can store multiple solutions in. The main advantage with an XDMFFile is that we only need to store the mesh once and that we can append multiple solutions to the same grid, reducing the storage space. The first argument to the XDMFFile is which communicator should be used to store the data. As we would like one output, independent of the number of processors, we use the COMM_WORLD. The second argument is the file name of the output file, while the third argument is the state of the file, this could be read ("r"), write ("w") or append ("a").

xdmf = io.XDMFFile(domain.comm, "diffusion.xdmf", "w")
xdmf.write_mesh(domain)

# Define solution variable, and interpolate initial solution for visualization in Paraview
uh = fem.Function(V)
uh.name = "uh"
uh.interpolate(initial_condition)
xdmf.write_function(uh, t)

Variational problem and solver#

As in the previous example, we prepare objects for time dependent problems, such that we do not have to recreate data-structures.

u, v = ufl.TrialFunction(V), ufl.TestFunction(V)
f = fem.Constant(domain, PETSc.ScalarType(0))
a = u * v * ufl.dx + dt * ufl.dot(ufl.grad(u), ufl.grad(v)) * ufl.dx
L = (u_n + dt * f) * v * ufl.dx

Preparing linear algebra structures for time dependent problems#

We note that even if u_n is time dependent, we will reuse the same function for f and u_n at every time step. We therefore call dolfinx.fem.form to generate assembly kernels for the matrix and vector.

bilinear_form = fem.form(a)
linear_form = fem.form(L)

We observe that the left hand side of the system, the matrix \(A\) does not change from one time step to another, thus we only need to assemble it once. However, the right hand side, which is dependent on the previous time step u_n, we have to assemble it every time step. Therefore, we only create a vector b based on L, which we will reuse at every time step.

A = assemble_matrix(bilinear_form, bcs=[bc])
A.assemble()
b = create_vector(linear_form)

Using petsc4py to create a linear solver#

As we have already assembled a into the matrix A, we can no longer use the dolfinx.fem.petsc.LinearProblem class to solve the problem. Therefore, we create a linear algebra solver using PETSc, assign the matrix A to the solver, and choose the solution strategy.

solver = PETSc.KSP().create(domain.comm)
solver.setOperators(A)
solver.setType(PETSc.KSP.Type.PREONLY)
solver.getPC().setType(PETSc.PC.Type.LU)

Visualization of time dependent problem using pyvista#

We use the DOLFINx plotting functionality, which is based on pyvista to plot the solution at every \(15\)th time step. We would also like to visualize a colorbar reflecting the minimal and maximum value of \(u\) at each time step. We use the following convenience function plot_function for this:

pyvista.start_xvfb()

grid = pyvista.UnstructuredGrid(*plot.vtk_mesh(V))

plotter = pyvista.Plotter()
plotter.open_gif("u_time.gif", fps=10)

grid.point_data["uh"] = uh.x.array
warped = grid.warp_by_scalar("uh", factor=1)

viridis = mpl.colormaps.get_cmap("viridis").resampled(25)
sargs = dict(title_font_size=25, label_font_size=20, fmt="%.2e", color="black",
             position_x=0.1, position_y=0.8, width=0.8, height=0.1)

renderer = plotter.add_mesh(warped, show_edges=True, lighting=False,
                            cmap=viridis, scalar_bar_args=sargs,
                            clim=[0, max(uh.x.array)])

Updating the solution and right hand side per time step#

To be able to solve the variation problem at each time step, we have to assemble the right hand side and apply the boundary condition before calling solver.solve(b, uh.x.petsc_vec). We start by resetting the values in b as we are reusing the vector at every time step. The next step is to assemble the vector calling dolfinx.fem.petsc.assemble_vector(b, L), which means that we are assembling the linear form L(v) into the vector b. Note that we do not supply the boundary conditions for assembly, as opposed to the left hand side. This is because we want to use lifting to apply the boundary condition, which preserves symmetry of the matrix \(A\) in the bilinear form \(a(u,v)=a(v,u)\) without Dirichlet boundary conditions. When we have applied the boundary condition, we can solve the linear system and update values that are potentially shared between processors. Finally, before moving to the next time step, we update the solution at the previous time step to the solution at this time step.

for i in range(num_steps):
    t += dt

    # Update the right hand side reusing the initial vector
    with b.localForm() as loc_b:
        loc_b.set(0)
    assemble_vector(b, linear_form)

    # Apply Dirichlet boundary condition to the vector
    apply_lifting(b, [bilinear_form], [[bc]])
    b.ghostUpdate(addv=PETSc.InsertMode.ADD_VALUES, mode=PETSc.ScatterMode.REVERSE)
    set_bc(b, [bc])

    # Solve linear problem
    solver.solve(b, uh.x.petsc_vec)
    uh.x.scatter_forward()

    # Update solution at previous time step (u_n)
    u_n.x.array[:] = uh.x.array

    # Write solution to file
    xdmf.write_function(uh, t)
    # Update plot
    new_warped = grid.warp_by_scalar("uh", factor=1)
    warped.points[:, :] = new_warped.points
    warped.point_data["uh"][:] = uh.x.array
    plotter.write_frame()
plotter.close()
xdmf.close()

error: XDG_RUNTIME_DIR is invalid or not set in the environment.
MESA: error: ZINK: failed to choose pdev
glx: failed to create drisw screen
gif

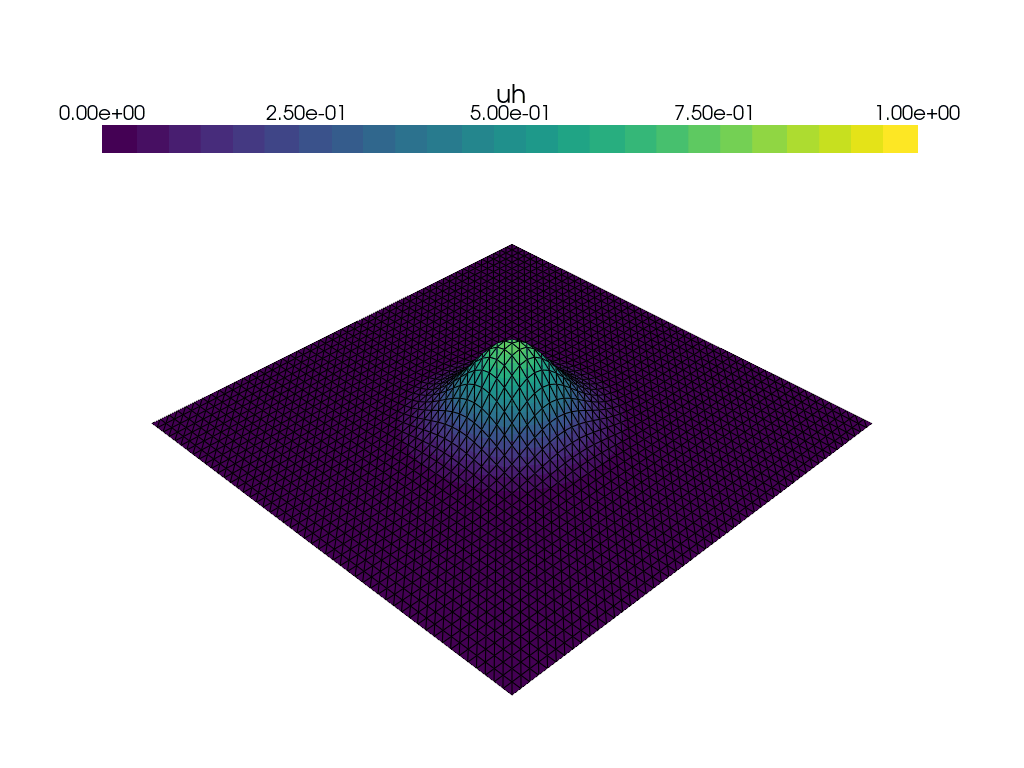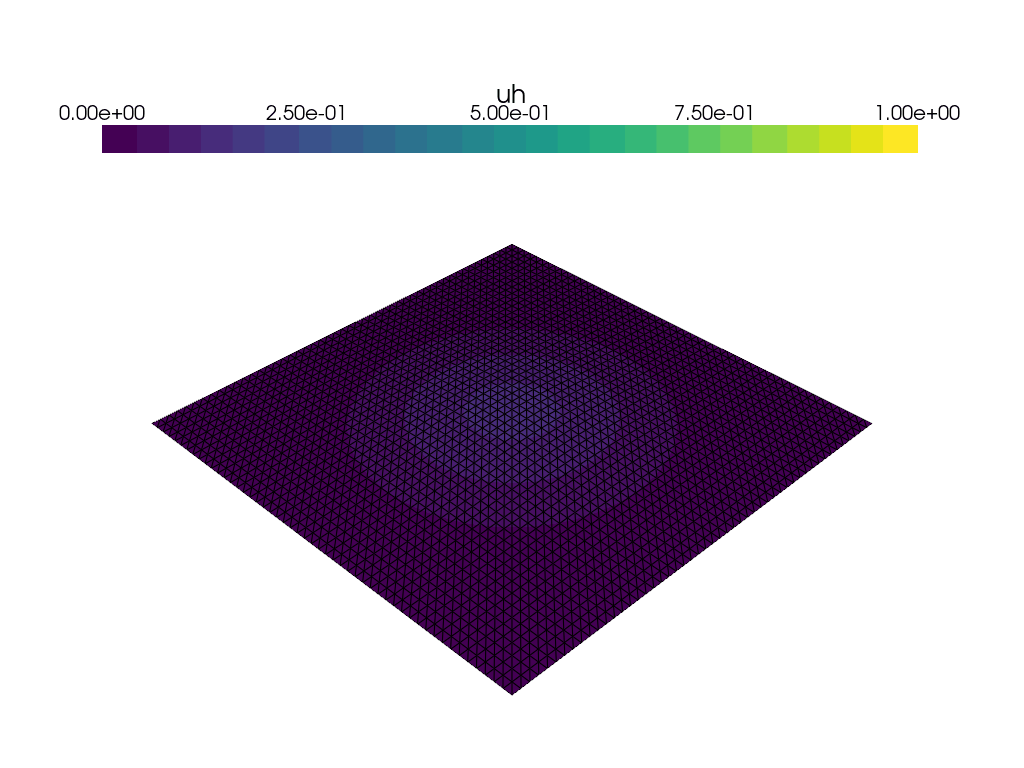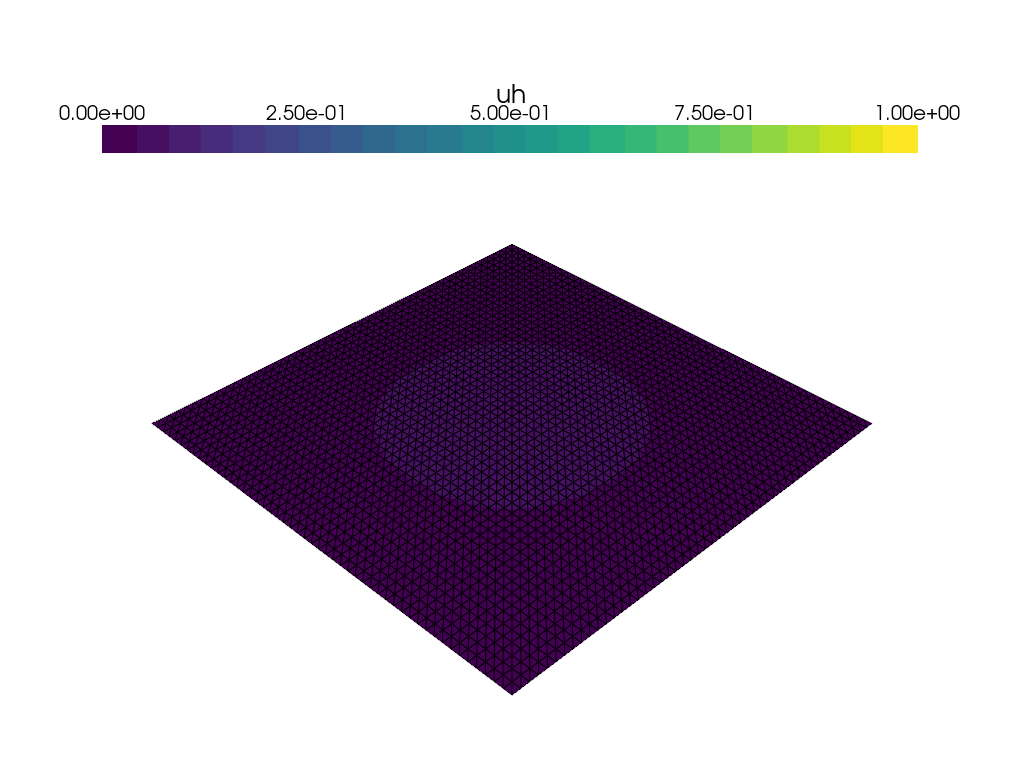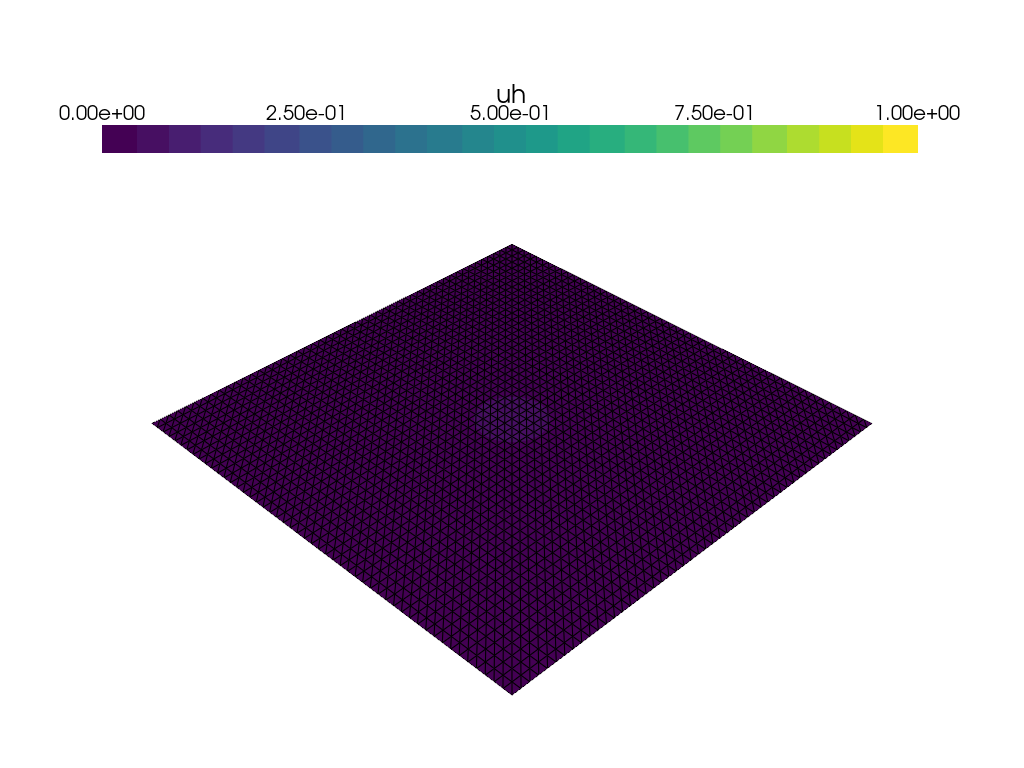
Animation with Paraview#

We can also use Paraview to create an animation. We open the file in paraview with File->Open, and then press Apply in the properties panel.

Then, we add a time-annotation to the figure, pressing: Sources->Alphabetical->Annotate Time and Apply in the properties panel. It Is also a good idea to select an output resolution, by pressing View->Preview->1280 x 720 (HD).

Then finally, click File->Save Animation, and save the animation to the desired format, such as avi, ogv or a sequence of pngs. Make sure to set the frame rate to something sensible, in the range of \(5-10\) frames per second.