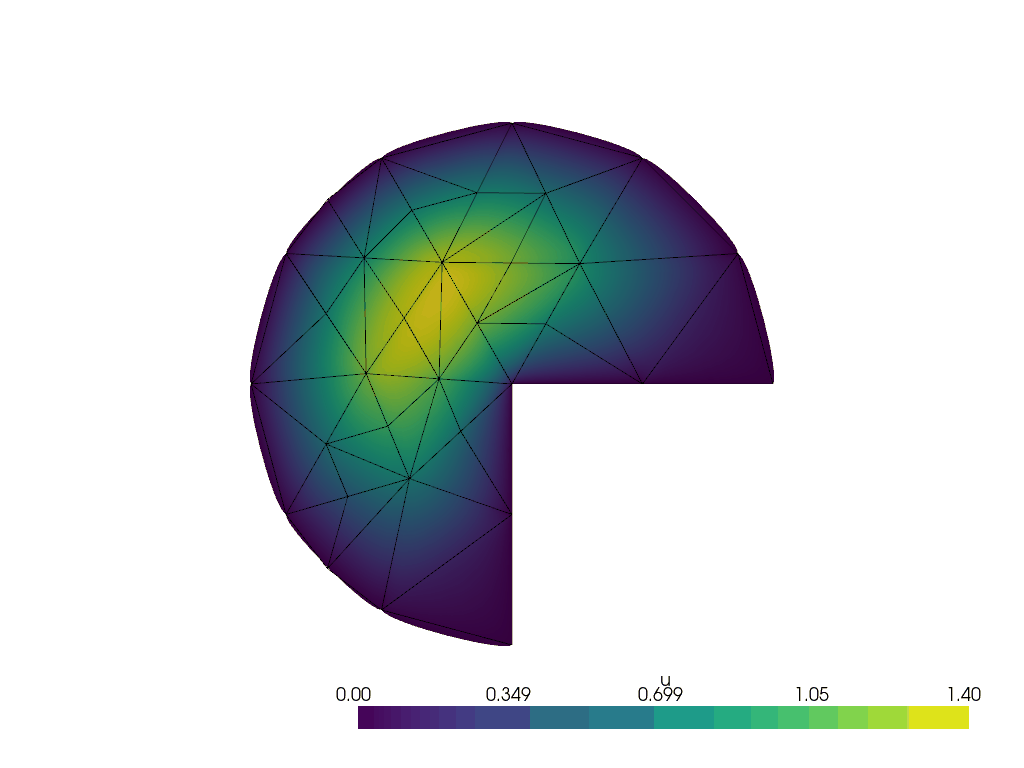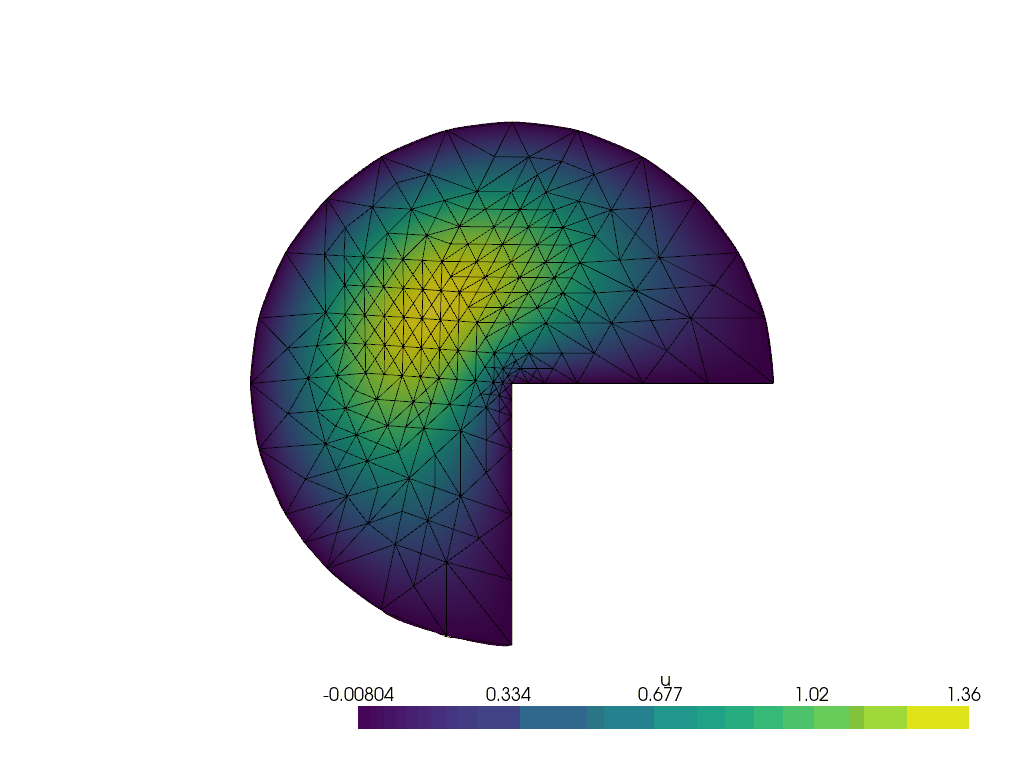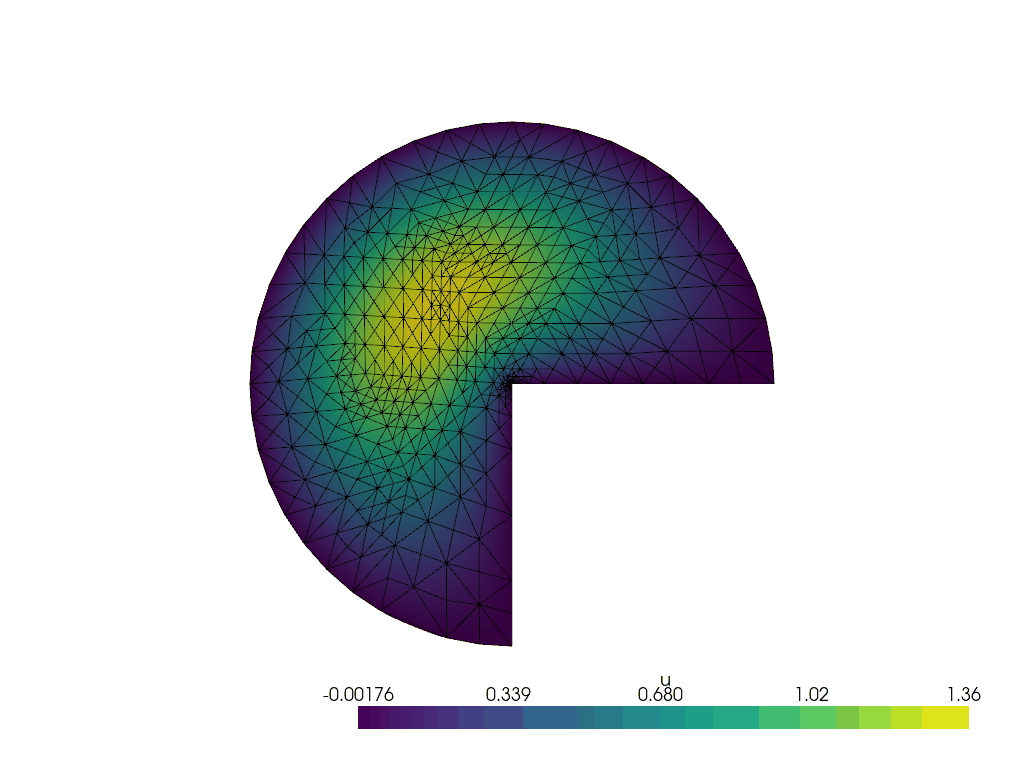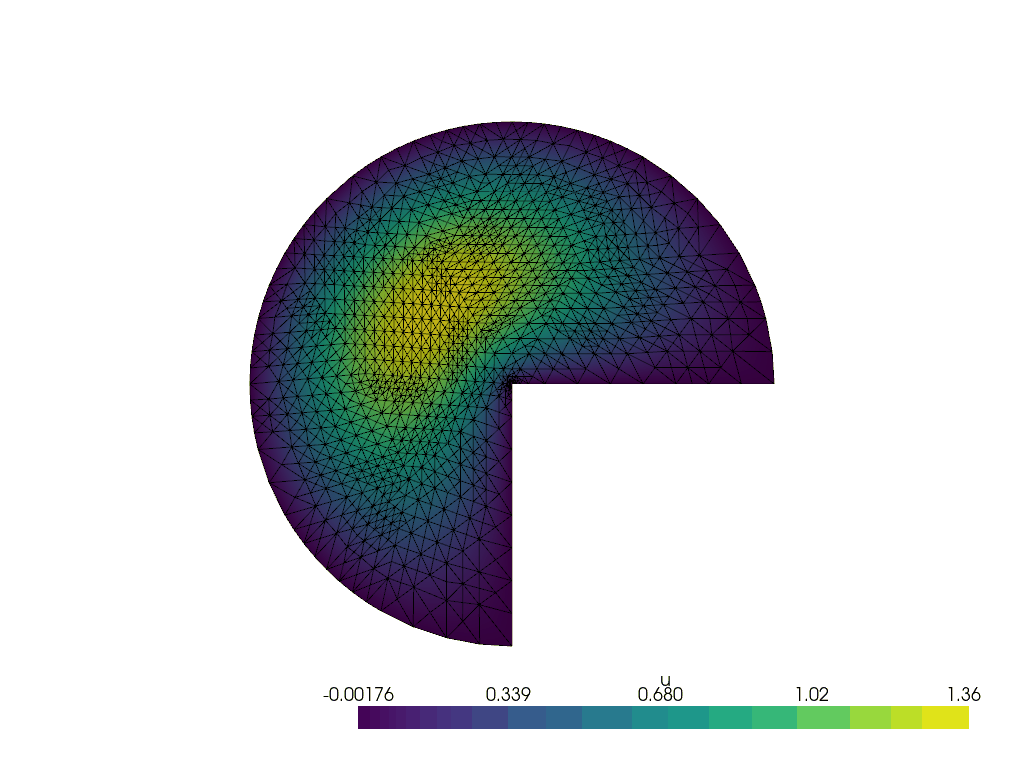Adaptive mesh refinement with NetGen and DOLFINx

Adaptive mesh refinement with NetGen and DOLFINx#

Author: Jørgen S. Dokken

NetGen and linux/arm64

NetGen is not available on PyPi on linux/arm64, so to run this tutorial on such machine, please use the docker image ghcr.io/jorgensd/dolfinx-tutorial:release. You can also install NetGen from source. See the Dockerfile for instructions.

In this tutorial, we will consider an adaptive mesh refinement method, applied to the Laplace eigenvalue problem. This demo is an adaptation of Firedrake - Adaptive Mesh Refinement. In this tutorial we will use the mesh generator NetGen from NGSolve. First, we import the packages needed for this demo:

from mpi4py import MPI
from petsc4py import PETSc
from slepc4py import SLEPc
from packaging.version import Version
import dolfinx.fem.petsc
import numpy as np
import ufl
import pyvista
import ngsPETSc.utils.fenicsx as ngfx

from netgen.geom2d import SplineGeometry

Generating a higher-order mesh with NetGen#

Next, we generate a PacMan-like geometry using NetGen.

geo = SplineGeometry()
pnts = [(0, 0), (1, 0), (1, 1), (0, 1), (-1, 1), (-1, 0), (-1, -1), (0, -1)]
p1, p2, p3, p4, p5, p6, p7, p8 = [geo.AppendPoint(*pnt) for pnt in pnts]
curves = [
    [["line", p1, p2], "line"],
    [["spline3", p2, p3, p4], "curve"],
    [["spline3", p4, p5, p6], "curve"],
    [["spline3", p6, p7, p8], "curve"],
    [["line", p8, p1], "line"],
]
for c, bc in curves:
    geo.Append(c, bc=bc)

Loading a mesh into DOLFINx#

The ngsPETSc package provides a communication layer between NetGen and DOLFINx. We initialize this layer by passing in a NetGen-model, as well as an MPI communicator, which will be used to distribute the mesh.

geoModel = ngfx.GeometricModel(geo, MPI.COMM_WORLD)

Next, we generate the mesh with the function :py:func:ngsPETSc.utils.fenicsx.GeometricModel.model_to_mesh. Which takes in the target geometric dimension of the mesh (2 for triangular meshes, 3 for tetrahedral), the maximum mesh size (hmax) and a few optional parameters.

mesh, (ct, ft), region_map = geoModel.model_to_mesh(gdim=2, hmax=0.5)

We use pyvista to visualize the mesh.

We have read in any cell and facet markers that have been defined in the NetGen model, as well as a map from their names to their integer ids in ct, ft and region_map respectively. We can curve the grids with the command curveField. In this example, we use third order Lagrange elements to represent the geometry.

order = 3
curved_mesh = geoModel.curveField(order)

Again, we visualize the curved mesh with pyvista.

Solving the eigenvalue problem#

In this section we will solve the eigenvalue problem:

Find \(u_h\in H_0^1(\Omega)\) and \(\lambda\in\mathbb{R}\) such that

\[ \begin{align} \int_\Omega \nabla u \cdot \nabla v~\mathrm{d} x &= \lambda \int_\Omega u v~\mathrm{d} x \qquad \forall v \in H_0^1(\Omega). \end{align} \]

Next, we define a convenience function to solve the eigenvalue problem using SLEPc given a discretized domain, its facet markers and the region map.

def solve(
    mesh: dolfinx.mesh.Mesh,
    facet_tags: dolfinx.mesh.MeshTags,
    region_map: dict[tuple[int, str], tuple[int, ...]],
) -> tuple[float, dolfinx.fem.Function, dolfinx.fem.Function]:
    # We define the lhs and rhs bilinear forms
    V = dolfinx.fem.functionspace(mesh, ("Lagrange", 3))
    u = ufl.TrialFunction(V)
    v = ufl.TestFunction(V)
    a = ufl.inner(ufl.grad(u), ufl.grad(v)) * ufl.dx
    m = ufl.inner(u, v) * ufl.dx

    # We identify the boundary facets and their corresponding dofs
    straight_facets = facet_tags.indices[
        np.isin(facet_tags.values, region_map[(1, "line")])
    ]
    curved_facets = facet_tags.indices[
        np.isin(facet_tags.values, region_map[(1, "curve")])
    ]
    boundary_facets = np.concatenate([straight_facets, curved_facets])
    mesh.topology.create_connectivity(mesh.topology.dim - 1, mesh.topology.dim)
    boundary_dofs = dolfinx.fem.locate_dofs_topological(
        V, mesh.topology.dim - 1, boundary_facets
    )

    # We create a zero boundary condition for these dofs to be in the suitable space, and
    # set up the discrete matrices `A` and `M`
    bc = dolfinx.fem.dirichletbc(0.0, boundary_dofs, V)
    A = dolfinx.fem.petsc.assemble_matrix(dolfinx.fem.form(a), bcs=[bc])
    A.assemble()
    if Version(dolfinx.__version__) < Version("0.10.0"):
        diag_kwargs = {"diagonal": 0.0}
    else:
        diag_kwargs = {"diag": 0.0}

    M = dolfinx.fem.petsc.assemble_matrix(dolfinx.fem.form(m), bcs=[bc], **diag_kwargs)
    M.assemble()

    # Next, we define the SLEPc Eigenvalue Problem Solver (EPS), and set up to use a shift
    # and invert (SINVERT) spectral transformation where the preconditioner factorisation
    # is computed using [MUMPS](https://mumps-solver.org/index.php).

    E = SLEPc.EPS().create(mesh.comm)
    E.setType(SLEPc.EPS.Type.ARNOLDI)
    E.setProblemType(SLEPc.EPS.ProblemType.GHEP)
    E.setDimensions(1, SLEPc.DECIDE)
    E.setOperators(A, M)
    ST = E.getST()
    ST.setType(SLEPc.ST.Type.SINVERT)
    PC = ST.getKSP().getPC()
    PC.setType("lu")
    PC.setFactorSolverType("mumps")
    E.setST(ST)
    E.solve()
    assert E.getConvergedReason() >= 0, "Eigenvalue solver did not converge"

    # We get the real and imaginary parts of the first eigenvector along with the eigenvalue.
    uh_r = dolfinx.fem.Function(V)
    uh_i = dolfinx.fem.Function(V)
    lam = E.getEigenpair(0, uh_r.x.petsc_vec, uh_i.x.petsc_vec)
    E.destroy()
    uh_r.x.scatter_forward()
    uh_i.x.scatter_forward()
    return (lam, uh_r, uh_i)

Error-indicator#

In this example, we will use an error-indicator \(\eta\) to decide what cells should be refined. Specifically, the estimator \(\eta\) is defined as:

\[\begin{align*} \eta^2 = \sum_{K\in \mathcal{T}_h(\Omega)}\left(h^2\int_K \vert \lambda u_h + \Delta u_h\vert^2~\mathrm{d}x\right) + \sum_{E\in\mathcal{F}_i}\frac{h}{2} \vert [\nabla \cdot \mathbf{n}_E ]\vert^2~\mathrm{d}s \end{align*}\]

where \(\mathcal{T}_h\) is the collection of cells in the mesh, \(\mathcal{F}_i\) the collection of interior facets (those connected to two cells).

def mark_cells(uh_r: dolfinx.fem.Function, lam: float):
    mesh = uh_r.function_space.mesh
    W = dolfinx.fem.functionspace(mesh, ("DG", 0))
    w = ufl.TestFunction(W)
    eta_squared = dolfinx.fem.Function(W)
    f = dolfinx.fem.Constant(mesh, 1.0)
    h = dolfinx.fem.Function(W)
    h.x.array[:] = mesh.h(mesh.topology.dim, np.arange(len(h.x.array), dtype=np.int32))
    n = ufl.FacetNormal(mesh)

    G = (  # compute cellwise error estimator
        ufl.inner(h**2 * (f + ufl.div(ufl.grad(uh_r))) ** 2, w) * ufl.dx
        + ufl.inner(h("+") / 2 * ufl.jump(ufl.grad(uh_r), n) ** 2, w("+")) * ufl.dS
        + ufl.inner(h("-") / 2 * ufl.jump(ufl.grad(uh_r), n) ** 2, w("-")) * ufl.dS
    )
    dolfinx.fem.petsc.assemble_vector(eta_squared.x.petsc_vec, dolfinx.fem.form(G))
    eta = dolfinx.fem.Function(W)
    eta.x.array[:] = np.sqrt(eta_squared.x.array[:])

    eta_max = eta.x.petsc_vec.max()[1]

    theta = 0.5
    should_refine = ufl.conditional(ufl.gt(eta, theta * eta_max), 1, 0)
    markers = dolfinx.fem.Function(W)
    ip = W.element.interpolation_points
    if Version(dolfinx.__version__) < Version("0.10.0"):
        ip = ip()
    markers.interpolate(dolfinx.fem.Expression(should_refine, ip))
    return np.flatnonzero(np.isclose(markers.x.array.astype(np.int32), 1))

Adaptive mesh refinement with NetGen and DOLFINx

Contents

Adaptive mesh refinement with NetGen and DOLFINx#

Generating a higher-order mesh with NetGen#

Loading a mesh into DOLFINx#

Solving the eigenvalue problem#

Error-indicator#

Running the adaptive refinement algorithm#